Lección

Estadística

Análisis de conglomerados o cluster

© Citar como: Salvador Figueras, M (2001): "Análisis de conglomerados o cluster", [en línea] 5campus.org, Estadística <http://www.5campus.org/leccion/cluster> [y añadir fecha consulta]este

 

1.- PLANTEAMIENTO DEL PROBLEMA

Sean X1,...,Xp  p variables numéricas observadas en n objetos.

Sea xij = valor de la variable Xj en el i-ésimo objeto  i=1,...,n; j=1,...,p.

El objetivo del Análisis Cluster es obtener grupos de objetos de forma que, por un lado, los objetos pertenecientes a un mismo grupo sean muy semejantes entre sí, es decir, que el grupo esté cohesionado internamente y, por el otro, los objetos pertenecientes a grupos diferentes tengan un comportamiento distinto con respecto a las variables analizadas, es decir, que cada grupo esté aislado externamente de los demás grupos.

Es una técnica eminentemente exploratoria puesto que la mayor parte de las veces, no utiliza ningún tipo de modelo estadístico para llevar a cabo el proceso de clasificación. Se la podría calificar como una técnica de aprendizaje no supervisado, es decir, una técnica muy adecuada para extraer información de un conjunto de datos sin imponer restricciones previas en forma de modelos estadísticos, al menos de forma explícita y, por ello, puede llegar a ser muy útil como una herramienta de elaboración de hipótesis acerca del problema considerado sin imponer patrones o teorías previamente establecidas.

Conviene, sin embargo, estar siempre alerta ante el peligro de obtener, como resultado del análisis, no una clasificación de los datos sino una disección de los mismos, en distintos grupos que sólo existen en la memoria del ordenador. El conocimiento que el analista tenga acerca del problema decidirá cuáles de grupos obtenidos son significativos y cuáles no.

En lo que sigue, analizaremos los pasos a seguir para llevar a cabo un Análisis Cluster, ilustrándolos con aplicaciones al Análisis Económico Internacional.

Ejemplo 1 (Clasificación de paises de la UE con datos binarios)

         En este ejemplo los datos corresponden a la situación de 6 países europeos en 1996 con respecto a los 4 criterios exigidos por la UE para entrar en la Unión Monetaria: Inflación, Interés, Déficit Público y Deuda Pública y vienen dados en la tabla  siguiente:

País

Inflación

Interés

Déficit

Deuda

Alemania

1

1

1

0

España

1

1

1

0

Francia

1

1

1

1

Grecia

0

0

0

0

Italia

1

1

0

0

Reino Unido

1

1

0

1

 

         Este es un ejemplo en el que todas las variables son binarias de forma que, este caso 1 significa que el país sí satisfacía el criterio exigido y 0 que no lo satisfacía.

Ejemplo 2  (Clasificación de paises de la UE con datos binarios)

         Este ejemplo corresponde a datos sobre diversas variables económicas, sanitarias y demográficas correspondientes a 102 países del mundo en el año 1995. Dichas variables vienen detalladas en la siguiente tabla:

Variable

Significado

POB

Logaritmo de la Población

DENS

Logaritmo de la Densidad

ESPF

Logaritmo de 83-Esperanza de vida Femenina

ESPM

Logaritmo de 78 - Esperanza de vida masculina

ALF

Logaritmo de 101-Tasa de Alfabetización

MINF

Logaritmo de la Tasa de Mortalidad Infantil

PIBCA

Logaritmo del PIB per cápita

NACDEF

Logaritmo de Nacimientos/Defunciones

FERT

Logaritmo del número medio de hijos por mujer

 

         En los dos ejemplos el objetivo es el mismo: encontrar grupos de países que muestren un comportamiento similar con respecto a las variables analizadas.

 

2. MEDIDAS DE PROXIMIDAD Y DE DISTANCIA

         Una vez establecidas las variables y los objetos a clasificar el siguiente paso consiste en establecer una medida de proximidad o de distancia entre ellos que cuantifique el grado de similaridad entre cada par de objetos.

Las medidas de proximidad, similitud o semejanza  miden el grado de semejanza entre dos objetos de forma que, cuanto mayor (resp. menor) es su valor, mayor (resp. menor) es el grado de similaridad existente entre ellos y con más (resp. menos) probabilidad los métodos de clasificación tenderán a ponerlos en el mismo grupo.

Las medidas de disimilitud, desemejanza o distancia miden la distancia entre dos objetos de forma que, cuanto mayor (resp. menor) sea su valor, más (resp. menos) diferentes son los objetos y menor (resp. mayor) la probabilidad de que los métodos de clasificación los pongan en el mismo grupo.

En la literatura existen multitud de medidas de semejanza y de distancia dependiendo del tipo de variables y datos considerados. En esta lección solamente veremos algunas de las más utilizadas. Para otros ejemplos  ver Anderberg (1973) o el manual de SPSS. 

Siguiendo el manual de SPSS podemos distinguir, esencialmente, los siguientes tipos de datos:

2.1 Tipos de datos

1)        De intervalo: se trata de una matriz objetosxvariables en donde todas las variables son cuantitativas, medidas en escala intervalo o razón

2)        Frecuencias: las variables analizadas son categóricas de forma que, por filas, tenemos objetos o categorías de objetos y, por columnas, las variables con sus diferentes categorías. En el interior de la tabla aparecen frecuencias.

3)        Datos binarios: se trata de una matriz objetosxvariables pero en la que las variables analizadas son binarias de forma que 0 indica la ausencia de una característica y 1 su presencia.

2.2 Medidas de proximidad

a) Medidas para variables cuantitativas

         1) Coeficiente de congruencia

crs =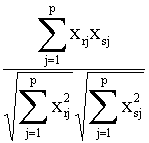

que es el coseno del ángulo que forman los vectores (xr1,...,xrp)' y (xs1,...,xsp)'.

         2) Coeficiente de correlación

rrs =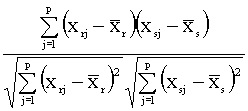

donde 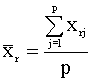  y .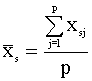

         Si los objetos r y s son variables, rrs mide el grado de asociación lineal existente entre ambas.

         Estas dos medidas se utilizan, preferentemente, para clasificar variables siendo, en este caso, invariantes por cambios de escala y, en el caso del coeficiente de correlación, invariante por cambio de origen. Por esta razón es más conveniente utilizar el coeficiente de congruencia con variables tipo razón en las cuales el origen está claramente definido.

         Conviene observar, además, que tanto crs como rrs toman valores comprendidos entre -1 y 1 pudiendo tomar, por lo tanto, valores negativos. Dado que, en algunos casos,  (por ejemplo, si los objetos a clasificar son variables), los valores negativos cercanos a -1 pueden implicar fuerte semejanza entre los objetos clasificados conviene, en estas situaciones, utilizar como medida de semejanza sus valore absolutos.        

b) Medidas para datos binarios     

         En este caso se construyen, para cada par de objetos r y s,  tablas de contingencia de la forma:

Objeto s\Objeto r

0

1

0

a

b

1

c

d

donde a = número de variables en las que los objetos r y s toman el valor 0, etc y p = a+b+c+d. Utilizando dichas tablas algunas de las medidas de semejanza más utilizadas son:

Coeficiente de Jacard: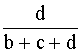

         Coeficiente de acuerdo simple: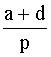

         Ambas toman valores entre 0 y 1 y miden, en tanto por uno, el porcentaje de acuerdo en los valores tomados en las p variables, existente entre los dos objetos. Difieren en el papel dado a los acuerdos en 0. El coeficiente de Jacard no los tiene en cuenta y el de acuerdo simple. Ello es debido a que, en algunas situaciones, las variables binarias consideradas son asimétricas en el sentido de que es más informativo el valor 1 que el valor 0. Así, por ejemplo, si el color de los ojos de una persona se codifica como 1 si tiene los ojos azules y 0 en caso contrario. En éste tipo de situaciones es más conveniente utilizar coeficientes tipo Jacard.

c) Medidas para datos nominales y ordinales

         Una generalización de las medidas anteriores viene dada por la expresión:

srs =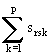

donde srsk es la contribución de la variable k-ésima a la semejanza total. Dicha contribución suele ser de la forma 1-drsk donde drsk es una distancia que suele tener la forma dklm siendo l el valor del estado de la variable Xk en el r-ésimo objeto y m el del s-ésimo objeto.

En variables nominales suele utilizarse dklm = 1 si l=m y 0 en caso contrario. En variables ordinales suele utilizarse medidas de la forma |l-m|r  con r>0.

2.3 Medidas de distancia

a) Medidas para variables cuantitativas

         Las más utilizadas son:

1) Distancia euclídea y distancia euclídea al cuadrado

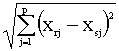y

2) Distancia métrica de Chebychev: maxi |xri-xsi|

                 3) Distancia de Manhattan:

         4) Distancia de Minkowski:   con qÎN.

Las tres primeras medidas son variantes de la distancia de Minkowski con q=2, ¥ y 1, respectivamente. Cuanto mayor es q más énfasis se le da a las diferencias en cada variable.

         Todas estas distancias no son invariantes a cambios de escala por lo que se aconseja estandarizar los datos si las unidades de medida de las variables no son comparables. Además no tienen en cuenta las relaciones existentes entre las variables. Si se quieren tener en cuenta se aconseja utilizar la distancia de Mahalanobis que viene dada por la forma cuadrática:

donde xr = (xr1,...,xrp)' y xs = (xs1,...,xsp)'

b) Medidas para tablas de frecuencias:

         Suelen estar basadas en la c2 de Pearson. Algunas de las más utilizadas son:

c2 =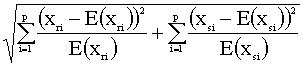

j2 =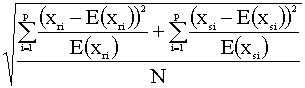

donde E(xri) = 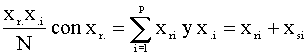 es el valor esperado de la frecuencia xri si hay independencia entre los individuos r y s y las categorías 1,...,p de las variables y N = xr.+xs. es el total de observaciones. La diferencia entre ambas medidas radica en la división por N en el caso de j2 para paliar la dependencia que tiene la c2 de Pearson respecto a N.

c) Medidas para datos binarios

         Las más utilizadas son:

         Distancia euclídea al cuadrado: b+c

         Lance y Williams: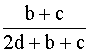

         Esta última ignora los acuerdos en 0.

d) Medidas para datos de tipo mixto

         Si en la base de datos existen diferentes tipos de variables: binarias, categóricas, ordinales, cuantitativas no existe una solución universal al problema de cómo combinarlas para construir una medida de distancia. Anderberg (1973) o Gordon (1990) sugieren las siguientes soluciones:

- Expresar todas las variables en una escala común, habitualmente binaria, transformando el problema en uno de los ya contemplados anteriormente. Esto tiene sus costes, sin embargo, en términos de pérdida de información si se utilizan escalas menos informativas como las nominales ú ordinales o la necesidad de incorporar información extra si se utilizan escalas más informativas como son las intervalo o razón.

- Combinar medidas con pesos de ponderación mediante expresiones de la forma:

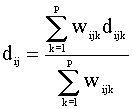
donde dijk es la distancia entre los objetos i y j en la k-ésima variable y wijk = 0 ó 1 dependiendo de si la comparación entre i y j es válida en la k-ésima variable

- Realizar análisis por separado utilizando variables del mismo tipo y utilizar el resto de las variables como instrumentos para interpretar los resultados obtenidos.

Ejempo 1 (continuación)

         En este caso todas las variables son binarias simétricas y podemos utilizar como medida de distancia la distancia euclídea al cuadrado. La matriz de distancias obtenida viene dada por:

 

Al

Es

Fr

Gr

It

RU

Al

0

0

1

3

1

2

Es

 

0

1

3

1

2

Fr

 

 

0

4

2

1

Gr

 

 

 

0

2

3

It

 

 

 

 

0

1

RU

 

 

 

 

 

0

 

         Así, por ejemplo, la distancia entre España y Francia es 1 puesto que solamente difieren en un criterio: el de la deuda pública que Francia satisfacía y España no.

Ejemplo 2 (continuación)

         En este caso todas las variables son cuantitativas pero medidas en diferentes unidades. Por esta razón utilizaremos la distancia euclídea pero con los datos estandarizados previamente.

3. MÉTODOS DE CLASIFICACIÓN

         Entre los muchos tipos de métodos que existen en la literatura cabe destacar los siguientes:

- Jerárquicos: en cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los de pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo

- Repartición: tienen un número de grupos, g fijado de antemano, como objetivo y agrupa los objetos para obtener los g grupos. Comienzan con una solución inicial  y los objetos se reagrupan de acuerdo con algún criterio de optimalidad.

- Métodos tipo Q: son similares al análisis factorial y utilizan como información la matriz XX’  utilizando las variables como objetos y los objetos como variables.

- Procedimientos de localización de modas: agrupan los objetos en torno a  modas con el fin de obtener zonas de gran densidad de objetos separadas unas de otras por zonas de poca densidad.

- Métodos que permiten solapamiento: permiten que los grupos tengan elementos en común.

         En esta lección prestaremos especial atención a los métodos jerárquicos aglomerativos y al algoritmo de las k-medias que es un caso particular de método de repartición.

3.1 Métodos jerárquicos

         Se caracterizan porque en cada paso del algoritmo sólo un objeto cambia de grupo y los grupos están anidados en los de pasos anteriores. Si un objeto ha sido asignado a un grupo ya no cambia más de grupo

         Pueden ser, a su vez de dos tipos: aglomerativos y divisivos.

         Los métodos aglomerativos comienzan con n clusters de un objeto cada uno. En cada paso del algoritmo se recalculan las distancias entre los grupos existentes y se unen los 2 grupos más similares o menos disimilares. El algoritmo acaba con 1 cluster conteniendo todos los elementos

         Los métodos divisivos comienzan con 1 cluster que engloba a todos los elementos. En cada paso del algortimo se divide el grupo más heterogéneo. El algoritmo acaba con n clusters de un elemento cada uno.

         Para determinar qué grupos se unen o dividen se utiliza una función objetivo o criterio que, en el caso de los métodos aglomerativos recibe el nombre de enlace.

3.1.1 Tipos de enlace

         Se utilizan con los métodos aglomerativos y proporcionan diversos criterios para determinar, en cada paso del algoritmo, qué grupos se deben unir. Cabe destacar los siguientes:

- Enlace simple o vecino más próximo

         Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más próximos o la similitud entre sus objetos más semejantes.

- Enlace completo o vecino más alejado

         Mide la proximidad entre dos grupos calculando la distancia entre sus objetos más lejanos o la similitud entre sus objetos menos semejantes

- Enlace medio entre grupos

Mide la proximidad entre dos grupos calculando la media de las distancias entre objetos de ambos grupos o la media de las similitudes entre objetos de ambos grupos. Así, por ejemplo, si se utilizan distancias, la distancia entre los grupos r y s vendría dada por:

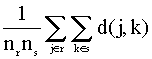
donde d(j,k) = distancia entre los objetos j y k y nr, ns son los tamaños de los grupos r y s, respectivamente.

-  Enlace medio dentro de los grupos

Mide la proximidad entre dos grupos con  la distancia media existente entre los miembros del grupo unión de los dos grupos. Así, por ejemplo, si se trata de distancias, la distancia entre los grupos r y s vendría dada por:

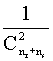
3.1.2 Métodos del centroide y de la mediana

         Ambos métodos miden la proximidad entre dos grupos calculando la distancia entre sus centroides

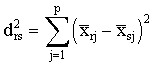
donde son las medias de la variable Xj en los grupos r y s, respectivamente.

         Los dos métodos difieren en la forma de calcular los centroides: el método del centroide utiliza las medias de todas las variables de forma que las coordenadas del centroide del grupo r = s È t vendrán dadas por:

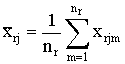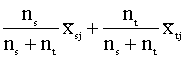=    j = 1,…,p

         En el método de la mediana el nuevo centroide es la media de los centroides de los grupos que se unen

= 

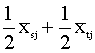
3.1.3 Método de Ward

         El método busca minimizar  donde SSWr es, para cada grupo r, las sumas de cuadrados intragrupo que viene dada por:

SSWr =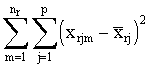

donde xrjm  denota el valor de la variable Xj en el m-ésimo elemento del grupo r.

         En cada paso del algoritmo une los grupos r y s que minimizan:

SSWt - SSWr - SSWs =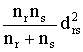

con t = r Ès y  la distancia entre los centroides de r y s.

3.1.4 Comparación de los diversos métodos aglomerativos

1) El enlace simple conduce a clusters encadenados

2) El enlace completo conduce a clusters compactos

3) El enlace completo es menos sensible a outliers que el enlace simple

4) El método de Ward y el método del enlace medio son los menos sensibles a outliers

5) El método de Ward tiene tendencia a formar clusters más compactos y de igual tamaño y forma en comparación con el enlace medio

6) Todos los métodos salvo el método del centroide satisfacen la desigualdad ultramétrica:

dut £ min {dur,dus}     t = r Ès

3.1.5 Elección del número de grupos

         Existen diversos métodos de determinación del número de grupos: algunos están basados en intentan reconstruir la matriz de distancias original, otros en los coeficientes de concordancia de Kendall y otros realizan analisis de la varianza entre los grupos obtenidos. No existe un criterio universalmente aceptado.

         Dado que la mayor parte de los paquetes estadísticos proporciona las distancias de aglomeración, es decir, las distancias a las que se forma cada grupo, una forma de determinar el número de grupos consiste en localizar en qué iteraciones del método utilizado dichas distancias pegan grandes saltos. Utilizando dichas distancias se pueden utilizar criterios como el criterio de Mojena que determina el primer sÎN tal que as+1 >  + ksa si se utilizan distancias y < si son similitudes donde {aj ;j=1,...,n-1} son las distancias de aglomeración, , sa su media y su desviación típica respectivamente y k una cte entre 2.5 y 3.5.

Ejemplo 1 (continuación)

         Los resultados de aplicar un método jerárquico aglomerativo con enlace completo utilizando el paquete estadístico SPSS 9.0 se muestran a continuación:

Dendograma

                                 Distancia de aglomeración reescalada

 

        C A S 0          0         5        10        15        20        25

  Etiqueta          Num  +---------+---------+---------+---------+---------+

 

  Alemania            1   -+-----------+

  España              2   -+           +-----------+

  Francia             3   -------------+           +-----------------------+

  Italia              5   -------------+-----------+                       I

  Reino Unido         6   -------------+                                   I

  Grecia              4   -------------------------------------------------+

 

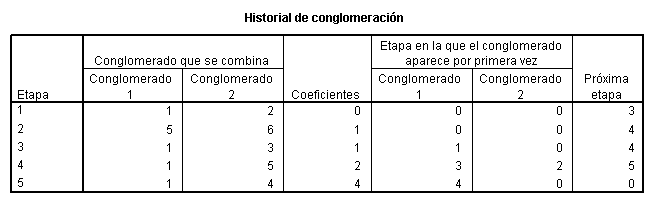
    El historial de aglomeración muestra las distancias de aglomeración y los grupos que se han ido formando al aplicar el algoritmo. El diagrama de témpanos y el dendograma dan dicha información de forma gráfica. Así, en el primer paso del algoritmo se unieron Alemania y España a una distancia de aglomeración igual a 0. Posteriormente, a dicho grupo, se unió Francia  e Italia y Reino Unido formaron otro grupo, todo ello a una distancia de aglomeración igual a 1. Estos dos grupos se unieron formando un único grupo a una distancia de aglomeración igual a 2. Finalmente Grecia se unió a todos los demás países a una distancia de aglomeración igual a 4, la máxima posible. Si tomamos como punto de corte 1 nos quedaríamos con 3 grupos: {España, Alemania y Francia}, {Italia, Reino Unido} y {Grecia}. Estos grupos están formados por países que difieren entre sí en a lo más un criterio.

Ejemplo 2 (continuación)

         En el gráfico 1 se muestran las distancias de aglomeración del algoritmo jerárquico aglomerativo tomando como función de enlace, el enlace intergrupos y utilizando el paquete estadístico SPSS 9.0

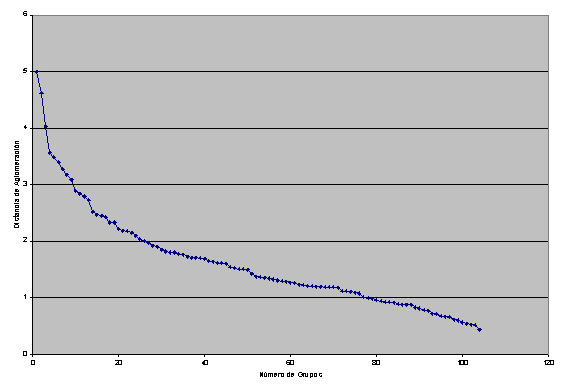
Gráfico 1: Distancias de aglomeración

         Se observa que los mayores saltos se dan cuando el algoritmo pasa de 4 a 3, 3 a 2 y 2 a 1 grupo. El criterio de Mojena aplicado con k=2.5 da una distancia de corte igual a 3.83 y selecciona un número de grupos igual a 4. Por todas estas razones tomamos como número de grupos 4.

3.2 Método de las k-medias

         Este tipo de método es conveniente utilizarlo cuando los datos a clasificar son muchos y/o para refinar una clasificación obtenida utilizando un método jerárquico. Supone que el número de grupos es conocido a priori.

Existen varias formas de implementarlo pero todas ellas siguen, básicamente, los siguientes pasos:

1)      Se seleccionan k centroides o semillas donde k es el número de grupos deseado

2)     Se asigna cada observación al grupo cuya semilla es la más cercana

3)     Se calculan los puntos semillas o centroides de cada grupo

4)     Se iteran los pasos 2) y 3) hasta que se satisfaga un criterio de parada como, por ejemplo, los puntos semillas apenas cambian o los grupos obtenidos en dos iteraciones consecutivas son los mismos.

El método suele ser muy sensible a la solución inicial dada por lo que es conveniente utilizar una que sea buena. Una forma de construirla es mediante una clasificación obtenida por un algoritmo jerárquico

Ejemplo 2 (continuación)

         Los resultados de aplicar el algoritmo de las k-medias implementado en SPSS 9.0, con un número de grupos igual a 4 y tomando como punto de partida los centroides de los grupos obtenidos anteriormente vienen dados por las siguientes tablas y gráficos. El algoritmo converge en 10 iteraciones y obtiene 4 grupos de tamaños 24, 39, 1 y 41 países respectivamente.

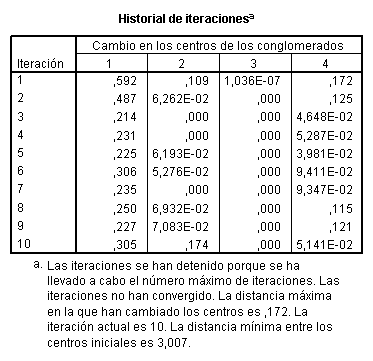
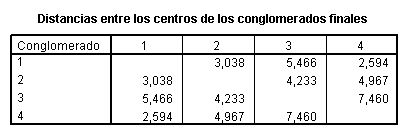
         En la tabla subsiguiente se muestran los países miembros de cada grupo junto con las distancias de cada país al centroide de su grupo. Así mismo se muestran las distancias entre los centroides de cada grupo. Se observa que los grupos 1 y 4 contienen países del tercer mundo, el grupo 2 está compuesto por países del primer y segundo mundos y el grupo 3 contiene únicamente a Islandia

Grupo obtenidos

PAIS

GRUPO

DISTANCIA

Venezuela

1

1,10992

Ecuador

1

1,17341

Malasia

1

1,19941

Panamá

1

1,24843

Acerbaján

1

1,27096

Colombia

1

1,31659

Armenia

1

1,33676

Chile

1

1,36857

Rep. Dominicana

1

1,49939

Turquía

1

1,57329

Uzbekistán

1

1,65333

Líbano

1

1,67326

México

1

1,69396

Tailandia

1

1,81748

El Salvador

1

1,81842

Corea del Norte

1

1,82812

Paraguay

1

1,88032

Jordania

1

1,90393

Argentina

1

2,05071

Emiratos Árabes

1

2,26097

Corea del Sur

1

2,28927

Costa Rica

1

2,56727

Kuwait

1

2,5803

Bahrein

1

2,78161

Austria

2

0,84751

Irlanda

2

1,02262

Dinamarca

2

1,03776

Croacia

2

1,17118

Bélgica

2

1,25977

Finlandia

2

1,29839

Grecia

2

1,39139

Polonia

2

1,39569

España

2

1,41288

Lituania

2

1,42745

Hungía

2

1,43235

Portugal

2

1,45946

Bielorusia

2

1,47973

Gran Bretaña

2

1,53294

Bulgaria

2

1,53866

Georgia

2

1,62389

Nueva Zelanda

2

1,68732

Suecia

2

1,69381

Rumanía

2

1,69529

Italia

2

1,71363

Alemania

2

1,71408

Países Bajos

2

1,77523

Noruega

2

1,83862

Uruguay

2

1,93886

Cuba

2

1,94022

Francia

2

1,98214

Estonia

2

2,01381

Letonia

2

2,02654

Suiza

2

2,04078

Ucrania

2

2,19731

Estados Unidos

2

2,30185

Canadá

2

2,60291

Australia

2

2,69585

Israel

2

2,71955

Rusia

2

2,89912

Japón

2

3,11629

Barbados

2

3,15042

Singapur

2

3,48935

Hong Kong

2

3,75342

Islandia

3

0,0000

Camerún

4

0,57933

Senegal

4

0,72504

Kenia

4

0,81205

Egipto

4

1,01448

Guatemala

4

1,07179

Camboya

4

1,17287

Marruecos

4

1,34473

Burkina Faso

4

1,35581

Nicaragua

4

1,40744

Tanzania

4

1,44743

Irán

4

1,45366

Nigeria

4

1,47222

Iraq

4

1,50176

Sudáfrica

4

1,51414

Perú

4

1,53181

Liberia

4

1,54648

Bolivia

4

1,56759

Uganda

4

1,57074

Honduras

4

1,58019

Zambia

4

1,58128

Etiopía

4

1,68095

Pakistán

4

1,69868

Afganistán

4

1,73597

Somalia

4

1,78696

Siria

4

1,86294

Haití

4

1,86689

Burundi

4

1,99972

Filipinas

4

2,03681

Indonesia

4

2,12085

Ruanda

4

2,13195

Vietnam

4

2,14496

Gambia

4

2,31622

Brasil

4

2,31901

Rep. C. Africana

4

2,41386

Arabia Saudí

4

2,4842

Bangladesh

4

2,5958

Libia

4

2,77066

Gabón

4

2,94421

India

4

2,96665

Botswana

4

2,96857

China

4

3,63459

 

 

 

 

4. INTERPRETACION DE LOS RESULTADOS

         Interpretar la clasificación obtenida por un Análisis Cluster requiere, en primer lugar, un conocimiento suficiente del problema analizado. Hay que estar abierto a la posibilidad de que no todos los grupos obtenidos tienen por qué ser significativos. Algunas ideas que pueden ser útiles en la interpretación de los resultados son las siguientes:

- Realizar ANOVAS y MANOVAS para ver qué grupos son significativamente distintos y en qué variables lo son

- Realizar Análisis Discriminantes. PONER ENLACE A PAGINA DE ANALISIS DISCRIMINANTE

- Realizar un Análisis Factorial o de Componentes Principales para representar, gráficamente los grupos obtenidos y observar las diferencias existentes entre ellos PONER ENLACES A FUTURAS PAGINAS WEB DE ESTOS DOS TEMAS

-         Calcular perfiles medios por grupos y compararlos.

Ejemplo 2 (continuación)

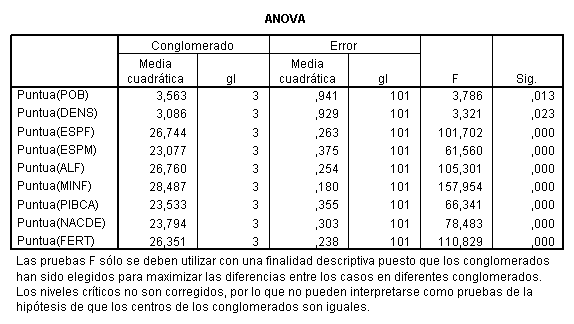
         En la tabla siguiente se muestran los resultados de aplicar un ANOVA para cada una de las variables analizadas. Se observa que existen diferencias significativas en todas las variables al 1 y al 5% con excepción de las variables POB y DENS en las que solamente existen diferencias al 5%.

         Los dos gráficos siguientes muestran los perfiles medio de cada grupo y los diagramas de cajas de las variables analizadas para cada uno de los grupos. Se observa que los países de los grupos 1 y 4 poseen una menor renta per cápita y peores indicadores los índices de alfabetización, mortalidad y esperanza de vida  así como una mayor fertilidad y natalidad que la de los países de los grupos 2 y 3 siendo estas diferencias más acusadas en los países del grupo 4 que la de los grupo 1. También queda de manifiesto el carácter atípico de Islandia debido a su baja natalidad, mortalidad infantil, población y densidad y su alta alfabetización, esperanza de vida.

 

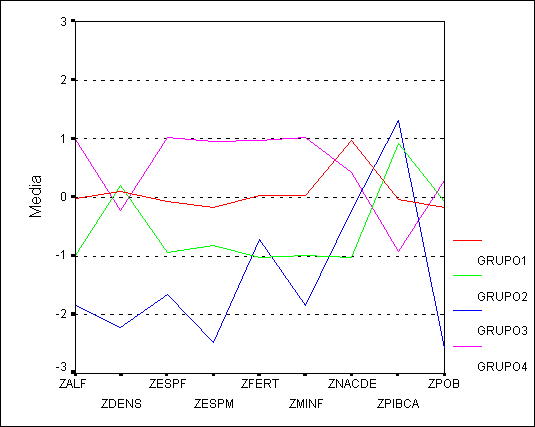
Gráfico 1: Perfiles medios de cada grupo

 

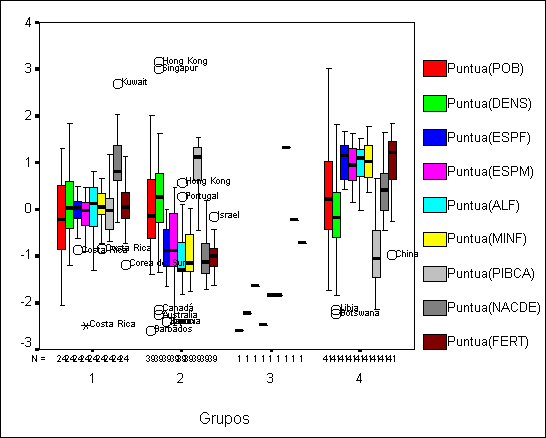
Gráfico 2: Diagrama de cajas correspondiente a cada grupo

 

5. VALIDACIÓN DE LA SOLUCIÓN

         Una vez obtenidos los grupos e interpretado los resultados conviene, siempre que sea posible, proceder a la validación de los mismos con el fin de averiguar, por un lado, hasta qué punto los resultados obtenidos son extrapolables a la población de la que vienen los objetos seleccionados y, por el otro, por qué han aparecido dichos grupos. Esta validación se puede realizar de forma externa o interna.

5.1 Validez interna

         Se puede establecer utilizando procedimientos de validación cruzada. Para ello se dividen los datos en dos grupos y se aplica el algoritmo de clasificación a cada grupo comparando los resultados obtenidos en cada grupo. Por ejemplo, si el método utilizado es el de las k-medias se asignaría cada objeto de uno de los grupos al cluster más cercano obtenido al clasificar los datos el otro grupo y se mediría el grado de acuerdo entre las clasificaciones obtenidas utilizando los dos métodos

5.2 Validez externa

         Se puede realizar comparando los resultados obtenidos con un criterio externo (por ejemplo, clasificaciones obtenidas por evaluadores independientes o analizando en los grupos obtenidos, el comportamiento de variables no utilizadas en el proceso de clasificación) o realizando un Análisis Cluster con una muestra diferente de la realizada.

Ejempo 2 (continuación)

         En los 3 gráficos siguientes se muestra la composición de cada grupo por religión mayoritaria, región económica y  clima predominante. Se observa que la mayor parte de los países cristianos pertenecen al grupo 2 siendo esta diferencia más clara en los cristianos ortodoxos y protestantes. Por otro lado, los países musulmanes y los que practican otras religiones  están en los grupos 1 y 4 . Los países budistas se distribuyen equitativamente en los 3 grupos

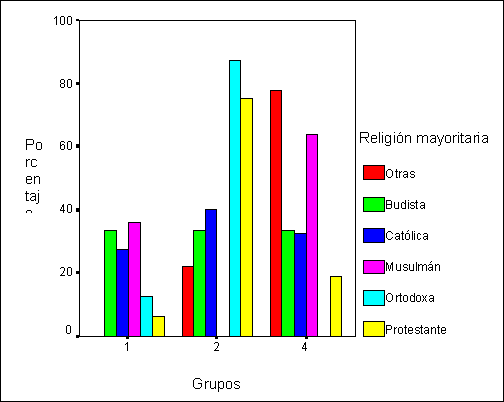
Gráfico 3: Composición de los grupos por religión

         Por regione económicas, los paises del primer y segundo mundos (OCDE y Europa Oriental) pertenecen todos al segundo grupo, los paises de América Latina y Oriente Medio tiende a estar en el grupo 1 mientras que todos los países africanos y la mayor parte de los paises de Asia están incluidos en el grupo 4. Los grupos reflejan, por lo tanto, las diferencias existentes entre las diversas regiones económicas del mundo

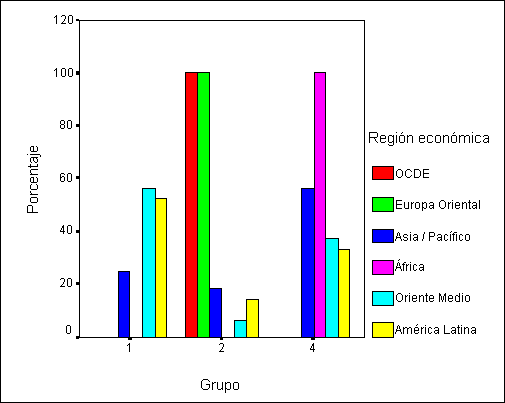
Gráfico 4: Composición de los grupos por región económica

 

         El gráfico 5 pone de manifiesto la influencia del clima en la composición de los grupos. La mayor parte de los países con climas templados y frío pertenecen al grupo 2 mientras que los países con clima desértico, ecuatorial y tropical tienden a estar en el grupo 4 y los de clima árido en el grupo 1.

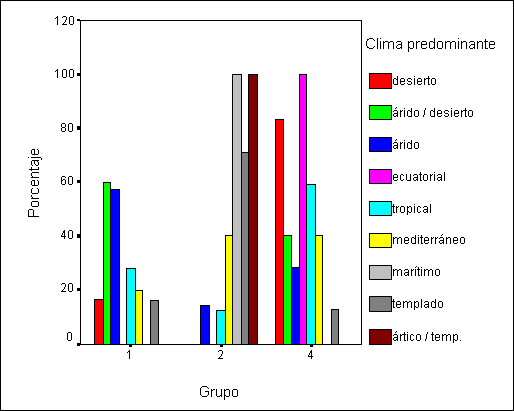
Gráfico 5: Composición de los grupos por clima predominante

 

 

Resumen

         El Análisis Cluster, también conocido como Análisis de Conglomerados, Taxonomía Numérica o Reconocimiento de Patrones, es una técnica estadística multivariante cuya finalidad es dividir un conjunto de objetos en grupos (cluster en inglés) de forma que los perfiles de los objetos en un mismo grupo sean muy similares entre sí (cohesión interna del grupo) y los de los objetos de clusters diferentes sean distintos (aislamiento externo del grupo).

         Para llevar a cabo un análisis de este tipo se deben los siguientes pasos:

1)     Plantear el problema a resolver por un Análisis Cluster

2)     Establecer medidas de semejanza y de distancia entre los objetos a clasificar en función del tipo de datos analizado

3)     Analizar algunos de los métodos de clasificación propuestos en la literatura haciendo especial énfasis en los métodos jerárquicos aglomerativos y en el algoritmo de las k-medias, y determinar el número de grupos.

4)     Interpretar los resultados obtenidos

5)     Analizar la validez de la clasificación obtenida

Conviene hacer notar, finalmente, que es una técnica eminentemente exploratoria cuya finalidad es sugerir ideas al analista a la hora de elaborar hipótesis y modelos que expliquen el comportamiento de las variables analizadas identificando grupos homogéneos de objetos. Los resultados del análisis deberían tomarse como punto de partida en la elaboración de teorías que explicquen dicho comportamiento.

Bibliografía

         Como libros de consulta dedicados exclusivamente al Análisis Cluster y con un montón de referencias adicionales recomiendo:

ANDERBERG, M.R. (1973). Cluster Analysis for Applications. Academic Press, New York

GORDON, A.D. (1999). Classification. 2nd Edition. Chapman and Hall.

KAUFMAN, L. and ROUSSEEUW, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis, Wiley, New York.

SNEATH, P.H. and SOKAL, R.R. (1973). Numerical Taxonomy, Freeman, San Francisco.

         Libros de Análisis Multivariantes que contienen buenos capítulos acerca del Análisis Discriminante.

         Desde un punto de vista más práctico:

AFIFI, A.A. and CLARK, V. (1996) Computer-Aided Multivariate Analysis. Third Edition. Texts in Statistical Science. Chapman and Hall.

EVERITT, B. And GRAHAM, D. (1991). Applied Multivariate Data Analysis. Arnold.

HAIR, J., ANDERSON, R., TATHAM, R. y BLACK, W. (1999). Análisis Multivariante. 5ª Edición. Prentice Hall.

SHARMA, S. (1998). Applied Multivariate Techiques. John Wiley and Sons.

URIEL, E. (1995). Análisis de Datos: Series temporales y Análisis Multivariante. Colección Plan Nuevo. Editorial AC.

 

         Desde un punto de vista más matemático:

 

JOBSON, J.D. (1992)  Applied Multivariate Data Analysis. Volume II: Categorical and Multivariate Methods. Springer-Verlag.

MARDIA, K.V., KENT, J.T. y BIBBY, J.M. (1994). Multivariate Analysis.  Academic Press.

 

         Enfocados hacia SPSS:

FERRAN, M. (1997). SPSS para WINDOWS. Programación y Análisis Estadístico. Mc.Graw Hill.

VISAUTA, B. (1998) Análisis Estadístico con SPSS para WINDOWS (Vol II. Análisis Multivariante).  Mc-Graw Hill.