- Ingresos mes, en euros
- Nivel de estudios, de 0 a 5
- 0=Sin estudios
- 1=Básico
- 2=Secundaria
- 3=Bachiller
- 4=Graduado Universidad
- 5=Máster
Y estos son los datos de 30 clientes (15 buenos y 15 malos):
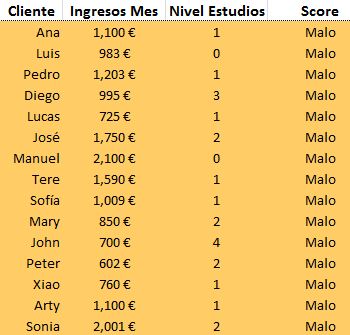
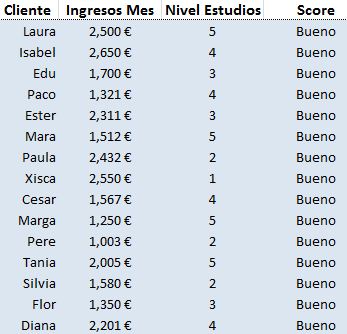
Juan gana 1800€ al mes y su nivel de estudios es Bachiller, es decir: 3

Queremos que el modelo de credit scoring clasifique a Juan como "bueno" o "malo".
Como solo son dos variables podemos visualizarlo mediante un diagrama de dispersión. Si tuviéramos más de dos variables no se podría. Para obtener el gráfico:
- Seleccionar el rango: cliente, ingesos y estudios
- Insertar gráfico -> XY Dispersión -> Solo marcadores
- Se trata de hacer tres series: malos, buenos y Juan
- Lo haremos en Diseño -> Seleccionar datos
- Editamos la primera serie, "Malos"
- En Nombre se escribe Malos
- En valores X se seleccionan los ingresos de los malos
- En valores Y se seleccionan los estudios
- Lo mismo con Buenos y con Juan
- Formato de serie, color rojo a los malos y resto
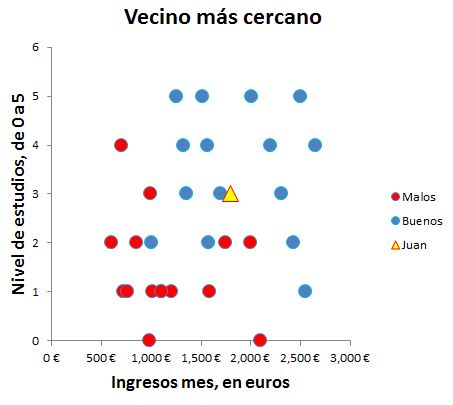
La ventaja es que podemos ver los vecinos de Juan. Pero esto es posible porque solo hay dos variables. Es necesario aplicar un algoritmo para cuando haya más variables.
El algoritmo KNN calcula la distancia entre Juan y sus vecinos. Si la mayor parte de sus vecinos son buenos clientes lo más probable es que sea un buen cliente. Es decir se basa en el refrán "Dime con quien andas y te diré quién eres".
Para calcular la distancia entre dos puntos A y B usamos el Teorema de Pitágoras.
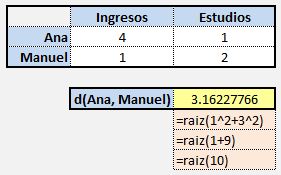
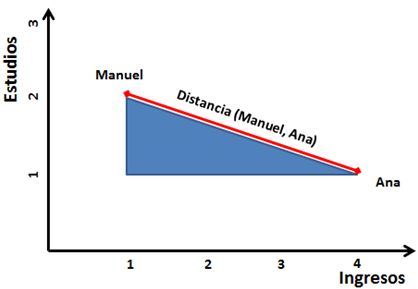
Si hay más de dos variables se calcula la distancia euclídea, que es el caso general:
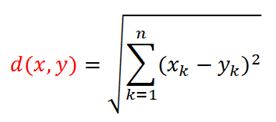
Pero hay un problema y es que el salario y el nivel de estudios están medidos en escalas diferentes. El salario mensual son miles de euros y el nivel de estudios va de 1 a 5. Entonces hay que normalizarlo, para que estén en la misma escala. Una forma es transformar tanto los ingresos como el nivel de estudio a la escala [0-1]. Así al que gana más (Isabel) le ponemos un 1 y al que gana menos (Peter) un 0. Es decir:
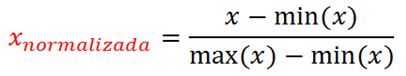
Normalizamos los datos de los clientes:
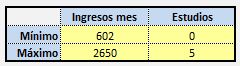
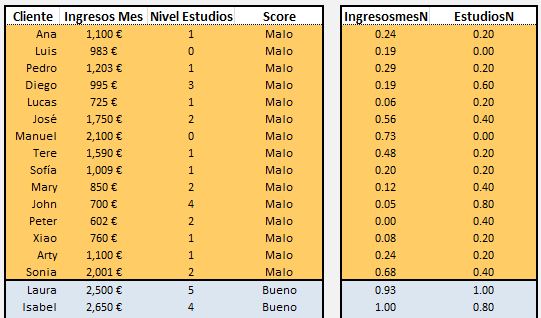
Calculamos la distancia con Juan, de cada uno de los clientes.
La función K.ESIMO.MENOR() permite saber cual es el menor, el segundo menor, etc.
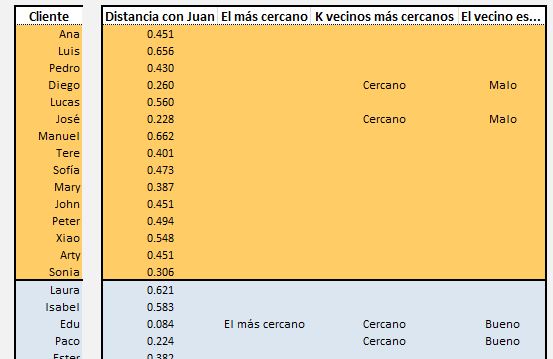
Tenemos que elegir el número de vecinos (K). Por ejemplo haremos K=7. Entonces el algoritmo selecciona los 7 vecinos más cercanos y contabiliza cuantos de ellos son "buenos" y cuantos son "malos".
Finalmente una condicional añade "bueno" si el número de vecinos buenos es mayor que el de malos o "malo" en caso contrario.

Para el icono se ha utilizado el tipo de letra Wingdings N (calavera) o J (cara sonriente).
Una empresa dispone de datos históricos de 15 clientes "buenos" y 15 "malos" y quiere realizar un credit scoring. Dispone de solo dos variables: los ingresos mensuales y el nivel de estudios. Naturalmente los credit scoring reales utilizan miles de datos y muchas variables, esto es solo un ejemplo.
![]() Descarga la hoja de cálculo con el ejercicio -> [08-CreditScoring.xls].
Descarga la hoja de cálculo con el ejercicio -> [08-CreditScoring.xls].