| Facultad de Economía y Empresa
Universidad de Zaragoza |
Préstamos |
Descargar la hoja de cálculo con el ejemplo -> [11-Prestamos.xls] |
¿Qué vamos a aprender?
- En esta hoja aprenderemos a manejar las funciones financieras de la hoja de cálculo relacionadas con los préstamos.
- Concretamente podremos calcular los pagos por intereses y devolución del principal en un préstamo tipo "francés".
- Lo haremos "a mano", aplicando la fórmula financiera y con las fórmulas de la hoja de cálculo.
Ingredientes:
- La funcion PAGO() calcula el pago de un préstamo basándose en pagos constantes y en una tasa de interés constante
- La funcion PAGOINT() calcula el interés pagado en un período basándose en pagos y tasa de interés constante
- La funcion PAGOPRIN() calcula el pago sobre el capital en un préstamos con pagos y tasa de interés constante
- Las funciones PAGO.INT.ENTRE() y PAGO.PRINC.ENTRE() calculan intereses y principal entre dos periodos
Pedimos un préstamo de 500.000€, durante 10 años, al 10% de intereses. Es un préstamo "francés", es decir, los términos amortizativos son constantes. ¿Cuánto pagaremos cada año?
Aplicaremos la función =PAGO(tasa;nper;va)
- Tasa es el tipo de interés del préstamo.
- Nper es el número total de pagos del préstamo.
- Va es el valor actual, o la cantidad total de una serie de futuros pagos.
- Vf es el valor futuro o un saldo en efectivo que se desea lograr después de efectuar el último pago. Si el argumento vf se omite, se supone que el valor es 0 (es decir, el valor futuro de un préstamo es 0).
- En Tipo se pone un 0 si los pagos vencen al final del período o un 1, si vencen al principio
Recordemos las fórmulas de la cuantía de una renta, que estudiamos en la lección correspondiente.
Por tanto, añadimos la función:
=PAGO(tasa;nper;va;vf;tipo)
--- > Cuantía.
Veamos el resultado.
Lo que paga cada periodo es la suma de los intereses más la devolución del préstamo. Vamos a verlo por partes.
Pedimos un préstamo de 500.000€, durante 10 años, al 10% de intereses. ¿Cuánto pagaremos de intereses el primer año?
Los intereses se calculan sobre el saldo. El primer año es fácil porque pagaremos el 10% de 500.000€, es decir 50.000€.
Pero para el resto de años necesitaremos construir una tabla en la que aparezca lo que vamos amortizando del préstamo cada año y sobre esta parte pagaremos los intereses. Esa tabla se llama "cuadro de amortización del préstamo" y la vemos más adelante.
No obstante, la hoja de cálculo tiene una función PAGOINT(). Esta función calcula el interés pagado en un período específico por una inversión basándose en pagos periódicos constantes y en una tasa de interés constante.
Su sintaxis es PAGOINT(tasa;período;nper;va;vf;tipo)
Todo ello es conocido excepto período que es el período para el que se desea calcular el interés y que debe estar entre 1 y el argumento nper.
Por ejemplo si queremos saber cuanto pagaremos de intereses el tercer año, será:
Pedimos un préstamo de 500.000€, durante 10 años, al 10% de intereses. ¿Cuánto pagaremos el primer año por la devolución del principal, es decir, por la amortización del préstamo?
Si anteriormente hemos calculado que el pago correspondiente a cada uno de los años era 81.372,70€ y que los intereses del primer año son 50.000€, entonces la diferencia entre ambas cantidades debe coincidir con la amortización, es decir, 31.372,70€.
Con la excel tenemos la funcion PAGOPRIN(), que devuelve el pago sobre el capital de una inversión durante un período determinado basándose en pagos periódicos y constantes, y en una tasa de interés constante.
Sus argumentos son PAGOPRIN(tasa;período;nper;va;vf;tipo).
¿Y el resto de años? En este caso también hay que hacer una tabla que veremos en el siguiente apartado. Pero con la función PAGOPRIN() es sencillo, con el argumento periodo.
Se pide calcular el cuadro de amortización de un préstamo de 500.000€, a devolver en 10 años y al 10% de interés anual. Calcular la TAE si hay una comisión de apertura del 1% y unos gastos fijos de estudio de 700€. En los flujos de caja hay que restar las comisiones y gastos.
Se pide calcular los intereses pagados entre dos periodos, concretamente entre el tercer y el sexto años. Si queremos calcular la suma de los intereses pagados entre dos periodos podemos usar PAGO.INT.ENTRE(). Se pide calcular los intereses pagados entre dos periodos, concretamente entre el tercer y el sexto años. Si queremos calcular la suma de los intereses y principal pagados entre dos periodos podemos usar PAGO.INT.ENTRE() y PAGO.PRINC.ENTRE(). Por ejemplo entre el periodo 3 y 6 sería.
Podemos obtener el mismo resultado simplementre sumando en la tabla anterior. Se pide calcular la TAE, hemos de tener en cuenta las comisiones. Se puede aplicar la función TASA() porque al ser un préstamo francés es una renta constante o TIR() porque tenemos los flujos de caja.
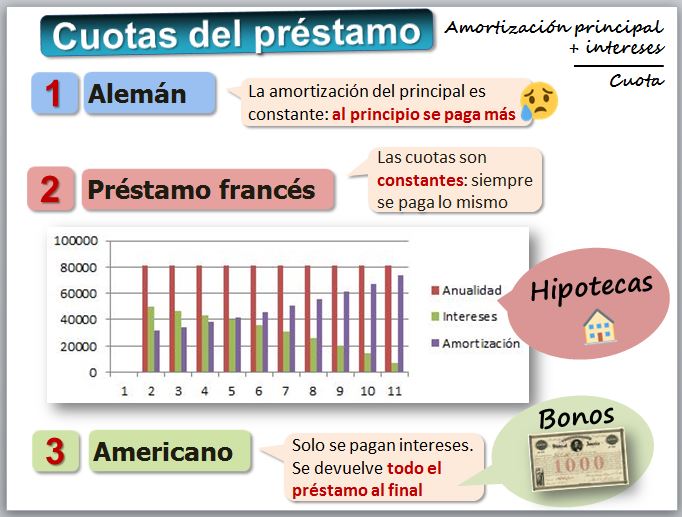
Finalmente podemos realizar ungráfico que nos muestra cada año la parte que destinamos a devolver el capital y la parte que destinamos al pago de intereses.
- Seleccionar el rango: anualidad, interés y amortización
- Insertar gráfico. Columna agrupada
- Insertar título
Nótese que al ser un préstamo francés la anualidad es constante y conforme se amortiza se pagan menos intereses.
Ejemplos en excel (http://www.masterfinanciero.es/p/prestamos.html) |
 Citar como: Serrano Cinca
C. (2021): "Lecciones de Finanzas",
[en línea] 5campus.org
<http://www.5campus.org/ifinanzas> [y añadir
fecha consulta] |
 [Índice] |
|---|
En este ejercicio se presenta un préstamo de tipo francés del que calcularemos las cuantías a pagar tanto por la amortización como por los intereses. Asimismo calcularemos la TAE. 
Para seguir aprendiendo