|
|
Análisis Discriminante
|
Citar
como: Salvador
Figueras, M (2000): "Análisis Discriminante", [en
línea] 5campus.com, Estadística
<http://www.5campus.com/leccion/discri> [y añadir fecha consulta]
1.-
PLANTEAMIENTO DEL PROBLEMA
Sea un
conjunto de n objetos divididos en q grupos {Gi;
i=1,...,q} de tamaños {ng;g=1,...,q}
que constituyen una partición de la
población de la que dichos objetos proceden.
Sea Y = (Y1,...,Yp)' un conjunto de variables numéricas observadas sobre dichos objetos
con el fin de utilizar dicha información para discriminar entre los q
grupos anteriores.
Mientras
no se diga lo contrario, supondremos que las variables anteriores son
cuantitativas.
Los
objetivos del Análisis Discriminante pueden sintetizarse en dos:
1) Analizar si existen
diferencias entre los grupos en cuanto a su comportamiento con respecto a las
variables consideradas y averiguar en qué sentido se dan dichas diferencias
2) Elaborar
procedimientos de clasificación sistemática de individuos de origen
desconocido, en uno de los grupos analizados.
Estos dos
objetivos dan lugar a dos ramas
dentro del Análisis Discriminante: el
Análisis Discriminante Descriptivo y el Análisis
Discriminante Predictivo, respectivamente.
En lo que
sigue, analizaremos los pasos a seguir para llevar a cabo ambos tipos de
análisis, ilustrándolos con los dos siguientes ejemplos que muestran una
aplicación del Análisis Discriminante al marketing basada en datos obtenidos
del libro de Hair et al. (1999) y una aplicación al análisis económico
internacional, respectivamente.
Ejemplo 1 (Discriminación con dos grupos)
Una empresa está interesada en analizar
la opinión de sus clientes con respecto a su labor comercial y de gestión. Para
ello realiza una encuesta a una muestra de 100 de ellos en las que le pide que
valoren su labor en los siguientes aspectos, haciendo una valoración entre 0 y
10: Velocidad de Entrega (VENTREGA), Nivel de Precios (NIVPREC), Flexibilidad
de Precios (FLEXPREC), Imagen de la Empresa (IMGEMPR), Servicio (SERVICIO),
Imagen de Ventas (IMGVENTA) y Calidad de Producto (CALIDAD).
Además, tiene clasificados a sus clientes en dos grupos de
acuerdo al tamaño de la empresa en la que trabajan: Empresas Pequeñas
(TAMAÑO=1) y Empresas Grandes (TAMAÑO=2).
El número de clientes pertenecientes a empresas pequeñas es igual a 60 y
el de empresas grandes es igual a 40.
El objetivo del estudio es analizar si existen diferencias
en cuanto a la percepción de su labor empresarial entre los clientes de un
grupo y del otro y, en caso de que existan, analizar en qué sentido se dan
dichas diferencias.
En este caso, por lo tanto, existen 7
variables clasificadoras (p=7) y dos grupos a discriminar (q=2). El tamaño de
la muestra es n=100 con n1
= 60 y n2
= 40.
Ejemplo
2 (Discriminación con 6 grupos)
En este ejemplo analizamos una base de datos
correspondiente a datos socio-económicos de 109 países del mundo del año 1995.
Dichos paises están clasificados de acuerdo a 6 regiones económicas: OCDE,
Europa Oriental, Asia/Pacífico, Africa, Oriente Medio y América Latina. Las
variables analizadas son el porcentaje de habitantes en ciudades (URBANA), el
aumento de la población (INCR_POB), la tasa de natalidad (TASA_NAT), la tasa de
mortalidad (TASA_MOR) y las transformaciones logarítmicas de la población
(LOGPOB), la densidad (LOGDENS), la esperanza de vida femenina (LOGESPF) y
masculina (LOGESPM), de la tasa de alfabetización (LOGALF), de la tasa de
mortalidad infantil (LOGMINF), del cociente nacimientos/muertes (LOGNACDE), de
la tasa de fertilidad (LOGFERT) y del PIB per cápita (LOGPIBCA).
En este caso se tiene, por lo tanto, que q=6, p=13 y
n=109. Además, n1=21,
n2 = 14, n3
= 17, n4 = 19, n5
= 17 y n6
= 21.
El objetivo del estudio es analizar si existen diferencias
entre las diversas regiones socio-económicas y, en caso afirmativo, en qué
sentido.
2.
CÁLCULO DE LAS FUNCIONES DISCRIMINANTES
La discriminación entre los q grupos se
realiza mediante el cálculo de unas funciones matemáticas denominadas funciones discriminantes. Existen varios
procedimientos para calcularlas siendo el procedimiento de Fisher uno de los
más utilizados que es el que exponemos, a continuación.
2.1 Procedimiento Discriminante de Fisher
El procedimiento de Fisher toma como
funciones discriminantes, combinaciones lineales de las variables
clasificadoras de la forma:
D
= u1Y1
+ u2Y2
+ ... + upYp
= u’Y
Sean
{dgk
k=1,…,ng; g=1,…,q} los
valores de la variable D en cada uno de los q grupos donde dgk
denota el valor de D en la k-ésima observación del g-ésimo grupo.
Sean 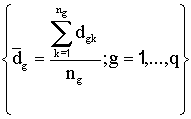 las medias muestrales
de la variable D en cada uno de los q grupos y sea
las medias muestrales
de la variable D en cada uno de los q grupos y sea 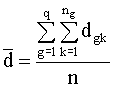 la media de la variable
D.
la media de la variable
D.
El procedimiento de Fisher determina el vector u
que maximiza el cociente:
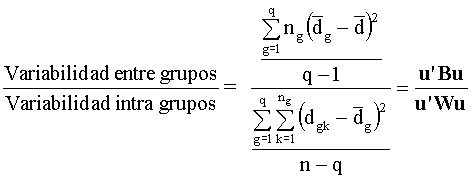
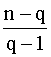
donde:
W
=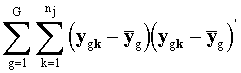 =
=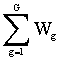 =
=
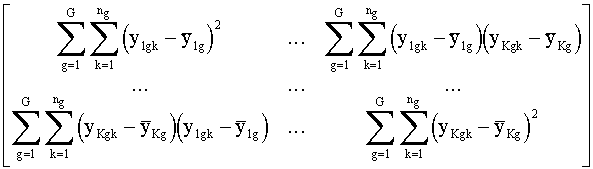
es
la matriz de suma de cuadrados intra-grupos
B
= 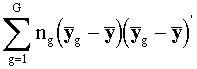 =
= 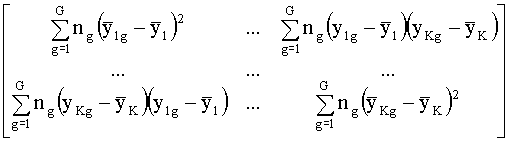
es la matriz de suma de cuadrados inter-grupos.
Se impone, además, la condición de normalizacion u’Wu
= 1
La solución viene dada por el vector propio u1
de W-1B
asociado al mayor valor propio l1
de esta matriz.
En general, si se quieren calcular r funciones
discriminantes con varianza 1, y que sean incorreladas entre sí, es decir, que
verifiquen que ui’Wuj
= dij
; i,j=1,…,r, se obtienen como soluciones los r vectores propios de W-1B
asociados a los r mayores valores propios de esta matriz l1
³
… ³
lr
> 0. A las funciones Di
= ui’Y
i=1,…,r se les llama funciones
discriminantes canónicas o funciones discriminantes de Fisher.
Observación
Si r es el número de funciones
discriminantes se tiene que WD
= Ir y BD
= diag(l1,…,lr) donde WD
y BD
son las matrices W y B
calculadas utilizando las puntuaciones discriminantes. Se sigue que:
li
= 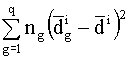 ; i=1,...,r
; i=1,...,r
donde
{![]() ; g=1,..,q} son las puntuaciones medias de la i-ésima función
discriminante en los q grupos y
; g=1,..,q} son las puntuaciones medias de la i-ésima función
discriminante en los q grupos y ![]() es la puntuación
media total.
es la puntuación
media total.
Por lo tanto, los valores propios {li
; i=1,...,r} miden el poder de discriminación de la i-ésima función
discriminante de forma que si li
= 0 la función discriminante no tiene ningún poder discriminante. Dado que el
rango de la matriz W-1B
es a lo más min{q-1,p} el número máximo de funciones discriminantes que se
podrán calcular será igual a min{q-1,p}.
2.2 Lambda de Wilks
Es un estadístico que mide el poder
discriminante de un conjunto de variables. Viene dada por
L =
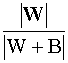 =
= 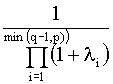
y
toma valores entre 0 y 1 de forma que, cuanto más cerca de 0 esté, mayor es el
poder discriminante de las variables consideradas y cuanto más cerca de 1,
menor es dicho poder.
Este estadístico tiene una distribución lambda de Wilks con p, q-1 y n-q grados de
libertad si se verifica la hipótesis nula:
Ho:
Y/Gi ~ Np(mi,S); i=1,...,q
con m1
= ... = mq
Û
Û Ho:
l1
= … = lmin{q-1,p}
= 0
2.3 Correlación canónica
La i-ésima correlación canónica viene dada por:
CRi
= 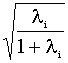 i = 1,...,r
i = 1,...,r
y
mide, en términos relativos, el poder discriminante de la i-esima función
discriminante ya que es el porcentaje de la variación total en dicha función
que es explicada por las diferencias entre los grupos.
Toma valores entre 0 y 1 de forma que,
cuanto más cerca de 1 esté su valor, mayor es la potencia discriminante de la
i-esima función discriminante.
2.4
Determinación del
número de funciones discriminantes
El número de funciones discriminantes
significativas se determina mediante un contraste de hipótesis secuencial.
Si denotamos por k=número de funciones
discriminantes significativas el proceso comienza con k=0. En el (k+1)-ésimo
paso del algoritmo la hipótesis nula a contrastar es
Ho:
lk+1
= … = lmin{G-1,p}
= 0
y
el estadístico de contraste viene dado por:
T = 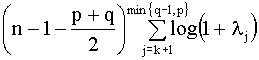
el
cual se distribuye como una c2(p-k)(q-k-1) si Ho
es verdad.
El p-valor asociado al contraste viene
dado por:
![]()
donde
Tobs es el valor observado de T.
El contraste para en el primer valor de
k para el cual la hipótesis nula Ho
se acepta.
Ejemplo1
(continuación)
En las tablas adjuntas se muestran los
valores de l1
= 2.046 y de la correlación canónica 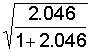 = 0.82 obtenidos mediante el programa SPSS 9.0. Así mismo, se
muestra el resultado obtenido al aplicar el test de hipótesis secuencial
utilizado para determinar el número de funciones discriminantes significativas.
En este caso el número máximo de funciones discriminantes posibles es igual a
min{2-1,7} = 1 por lo que sólo será necesario llevar a cabo un test de
hipótesis.
= 0.82 obtenidos mediante el programa SPSS 9.0. Así mismo, se
muestra el resultado obtenido al aplicar el test de hipótesis secuencial
utilizado para determinar el número de funciones discriminantes significativas.
En este caso el número máximo de funciones discriminantes posibles es igual a
min{2-1,7} = 1 por lo que sólo será necesario llevar a cabo un test de
hipótesis.
La hipótesis nula será Ho:
l1
= 0 y el valor del estadístico T=105.244 correspondiente a una lambda de Wilks
igual a 0.328. El p-valor es igual a ![]() =0.000 por lo que la función obtenida es significativa y su
poder discriminante es alto dado el elevado valor de la correlación canónica.
=0.000 por lo que la función obtenida es significativa y su
poder discriminante es alto dado el elevado valor de la correlación canónica.
Resumen de las funciones canónicas discriminantes


Ejemplo 2 (continuación)
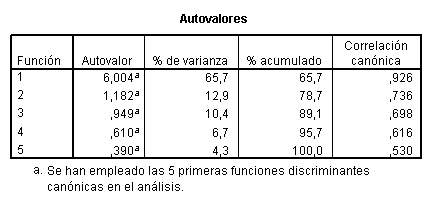
En este caso el número de funciones
discriminantes calculadas es igual a min{6-1,13}=5. En las tablas subsiguientes
se muestran los valores propios, la correlación canónica y el porcentaje de
varianza de discriminación y el porcentaje acumulado explicados por cada
función discriminante, los cuales vienen dados por 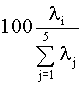 y
y 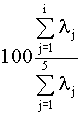 respectivamente. Se
observa, por ejemplo, que las 3 primeras funciones discriminantes explican un
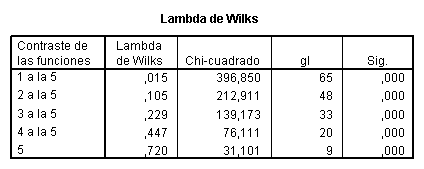
89.1% de la varianza de discriminación. Así mismo, en la siguiente tabla se
realiza el contraste para la determinación del número de funciones
discriminantes significativas. Así, por ejemplo, en el paso 3 se contrasta la
hipótesis nula:
respectivamente. Se
observa, por ejemplo, que las 3 primeras funciones discriminantes explican un
89.1% de la varianza de discriminación. Así mismo, en la siguiente tabla se
realiza el contraste para la determinación del número de funciones
discriminantes significativas. Así, por ejemplo, en el paso 3 se contrasta la
hipótesis nula:
Ho:
l3
= l4
= l5
En este caso Tobs
= 139.173 y el p-valor ![]() =0 y se rechazaría la hipótesis nula. Se observa que todas
las funciones discriminantes son significativas.
=0 y se rechazaría la hipótesis nula. Se observa que todas
las funciones discriminantes son significativas.
Resumen de las funciones canónicas discriminantes
3. INTERPRETACIÓN DE LOS RESULTADOS
Los
resultados obtenidos se interpretan desde dos ópticas:
-
Significado de las dimensiones de discriminación
entre los grupos proporcionadas por las funciones discriminantes mediante el
análisis de la matriz de estructura y de la de los coeficientes estandarizados
de las funciones discriminantes.
-
Análisis del sentido de la discriminación entre
dichos grupos, es decir, averiguar qué grupos separa cada función discriminante
y en qué sentido. Este análisis se lleva a cabo mediante representaciones
gráficas del espacio de discriminación así como de perfiles multivariantes
correspondientes a cada grupo.
3.1 Matriz de estructura
Es una matriz pxr que contiene, por filas, los
coeficientes de correlación de las
funciones discriminantes con las variables originales. De esta forma es posible
interpretar el significado de las mismas utilizando, para cada una de ellas,
aquéllas variables con las que está más correlacionada. De cara a facilitar
dicha interpretación se suelen realizar rotaciones ortogonales del espacio de
discriminación similares a las utilizadas por el Análisis Factorial.
3.2 Coeficientes estandarizados de
las funciones discriminantes
Vienen dados por la expresión:
u* = F-1u
donde
F = ![]() siendo sjj
elemento de la diagonal de la matriz
siendo sjj
elemento de la diagonal de la matriz ![]() . A partir de ellos se puede deducir la expresión matemática
de las funciones discriminantes en términos de las variables originales
estandarizadas. Estos coeficientes son poco fiables si existen problemas de
multicolinealidad entre las variables clasificadoras.
. A partir de ellos se puede deducir la expresión matemática
de las funciones discriminantes en términos de las variables originales
estandarizadas. Estos coeficientes son poco fiables si existen problemas de
multicolinealidad entre las variables clasificadoras.
Ejemplo 1 (continuación)
En
las tablas subsiguientes se muestran los coeficientes estandarizados de la
función discriminante estimada así como la matriz de estructura. La expresión
mátemática de dicha función vendrá dada por:
D
= 0.466Zventrega
+ 0.084Znivprec
+0.538Zflexprec-0.068Zimgempr
-0.093Zservicio+0.295Zimgventa-0.6784Zcalidad
donde
Zi indica la tipificación de la
variable i-ésima.
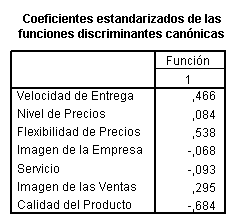

Analizando
la matriz de estructura de la función discriminante se observa que dicha
función realiza un contraste entre la Velocidad de Entrega y la Flexibilidad de
Precios, por un lado, y la Calidad del Producto y el Nivel de Precios, por el
otro, de forma que clientes con un valor de D positivo serán clientes con una
tendencia a valorar por encima de la media a la labor de la empresa en aspectos
más específicos como rapidez y flexibilidad y a valorar por debajo aspectos más
genéricos como son la calidad del producto y el nivel de precios. Lo contratrio
ocurre con clientes con valores de D negativos.
La siguiente tabla contiene las
puntuaciones medias ![]() ;i=1,2 para cada grupo.
;i=1,2 para cada grupo.

y
el gráfico subsiguiente los diagramas de caja de dichas puntuaciones
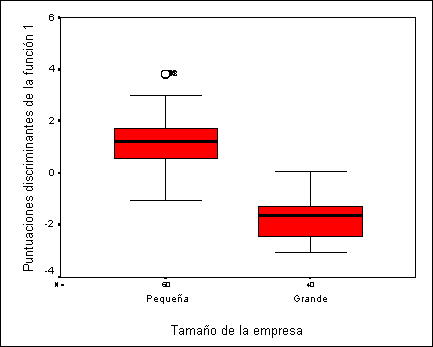
Se observa que, las empresas pequeñas,
tienden a valorar mejor a la empresa en aspectos más específicos como son la
velocidad de entrega y flexibilidad de precios y, por el contrario, las
empresas grandes tienden a valorar mejor los aspectos más generales como son el
nivel de precios y la calidad del producto ofrecido. Estos resultados se
confirman al comparar los diagramas de caja de cada una de las variables en los
dos grupos como se muestra en el gráfico siguiente
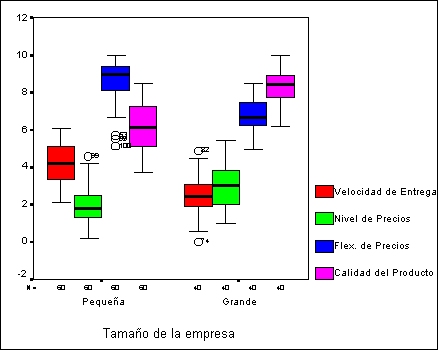
Ejemplo
2 (continuación)
En la tabla
subsiguiente se muestra la matriz de estructura de las funciones discriminantes
tras aplicar una rotación varimax. Se observa que la primera función discrimina
en función del equilibrio demográfico existente en cada país, la segunda tiene
que ver con aspectos relacionados con el crecimiento demográfico del mismo, la
tercera con su calidad de vida y la quinta con su tamaño demográfico. La cuarta
función, cuyo poder discriminante no es muy alto, no ofrece una interpretación
tan clara aunque parece estar relacionado con el nivel de desarrollo
económico-cultural del país debido a su mayor correlación con PIBPCA, Habitantes en ciudades y tasa de alfabetización.
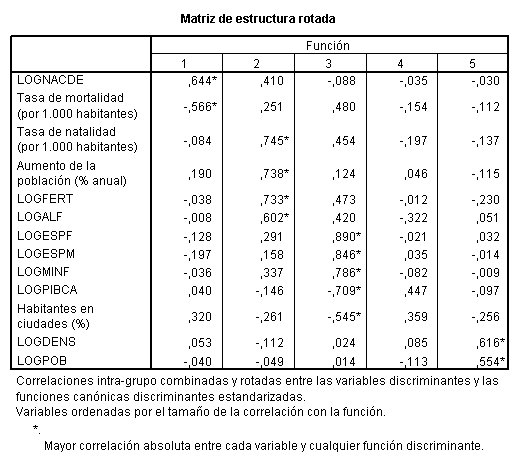
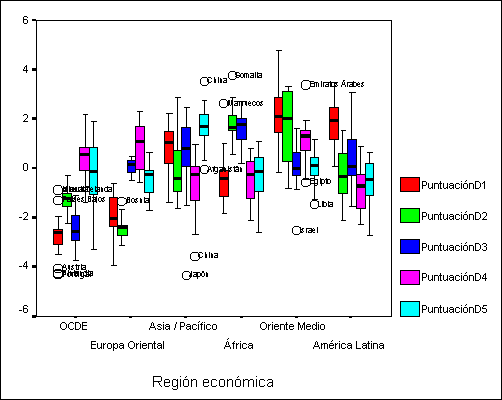
En
el gráfico siguiente se muestra el diagrama de cajas de las puntuaciones
discriminantes estimadas para cada uno de los países clasificados por región
económica.
Se observa que las dos primeras funciones
discriminantes separan, esencialmente, a los países de la OCDE y de la Europa
Oriental del resto debido al mayor equilibrio demográfico existente en las dos
regiones anteriores por su baja natalidad y su baja mortalidad. La tercera
función separa a los países de la OCDE debido a su mayor nivel de vida que se
traduce en una mayor esperanza de vida, un mayor PIB per cápita y un mayor
porcentaje de hombres y mujeres viviendo en ciudades. La cuarta función
discrimina, esencialmente a las regiones más pobres y menos desarrolladas
(Asia/Pacífico, Africa y América Latina) frente a las más ricas y menos
desarrolladas (OCDE, Europa Oriental y Oriente Medio)
La
quinta función separa a los países asiáticos del resto debido a su mayor
población y su mayor densidad. Respecto a la cuarta no se ve un patrón claro de
separación.
La siguiente figura muestra los
perfiles multivariantes de cada región los cuales corroboran las
interpretaciones anteriores.

4.- SELECCIÓN DE VARIABLES CLASIFICADORAS
El
problema de selección de variables intenta responder a la pregunta ¿Son
necesarias todas las variables clasificadoras para discriminar?
Para
responderla existen, esencialmente,
tres tipos de algoritmos: algoritmos de selección de variables hacia adelante,
eliminación hacia atrás y de regresión por pasos.
Los algoritmos de selección hacia adelante comienzan
eligiendo la variable que más discrimina entre los q grupos. A continuación
seleccionan la segunda más discriminante y así sucesivamente. Si de las
variables que quedan por elegir ninguna discrimina de forma significativa entre
los grupos analizados el algoritmo finaliza.
Los algoritmos de eliminación hacia detrás proceden
de forma inversa a los anteriores. Se comienza suponiendo que todas las
variables son necesarias para discriminar y se elimina la menos discriminante
entre los grupos analizados y así sucesivamente. Si las variables no eliminadas
discriminan significativamente entre los grupos analizados el algoritmo
finaliza.
Los algoritmos de regresión por pasos
utilizan una combinación de los dos algoritmos anteriores permitiendo la
posibilidad de arrepentirse de decisiones tomadas con precipitación bien sea
eliminando del conjunto seleccionado una variable introducida en el conjunto de
discriminación en un paso anterior del algoritmo, bien sea introduciendo en
dicho conjunto una variable eliminada con anterioridad.
Para
determinar qué variables entran y salen en cada paso de este tipo de algoritmos
se utilizan diversos criterios de entrada y salida. Uno de los más utilizados
es el de la lambda de Wilks que es el que exponemos, a continuación. Otros
criterios pueden verse, por ejemplo, en el manual del SPSS 9.0.
4.1 Criterio de la
lambda de Wilks
Utiliza la
lambda de Wilks para medir la potencia discriminante ganada/perdida al
introducir/sacar una variable del conjunto de discriminación.
Sea Lq
la lambda de Wilks basada en las q primeras variables.
Para ver si
es necesario incluir la variable Yq+1
en el conjunto de discriminación se utiliza el estadístico
F = 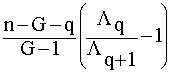 ~ FG-1,n-G-q
~ FG-1,n-G-q
si la variable Yq+1
no aporta información relevante al proceso de discriminación entre los grupos.
Un valor alto/bajo de F indica una pérdida significativa/no significativa de
información si la variable Yq+1
no es incluida/es incluida en el conjunto de discriminación.
Utilizando
dicha variable es posible, por ejemplo, proporcionar un p-valor de entrada y
otro de salida de forma que si el p-valor obtenido al introducir una variable
en el conjunto de discriminación, no es inferior al p-valor de entrada, la
variable considerada no entra en dicho conjunto y si el p-valor obtenido al
eliminarla del conjunto de discriminación no es superior al de salida, la
variable considerada no sale de dicho conjunto.
Ejemplo 1 (continuación)
En las
tablas subsiguientes se muestran los resultados obtenidos al aplicar el
algoritmo de selección de variables utilizado por SPSS 9.0. tomando como
criterio de entrada un p-valor igual a 0.05 y como criterio de salida un
p-valor igual a 0.10. Las variables seleccionadas son (por orden de selección)
la calidad del producto, la flexibilidad de precios y la velocidad de entrega
no siendo eliminada del conjunto de discriminación, ninguna de las variables
seleccionadas.
Estadísticos por pasos
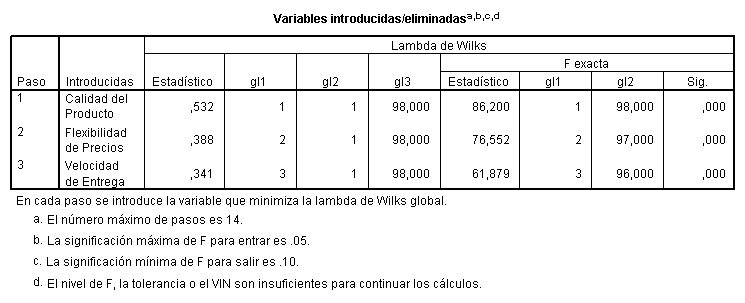

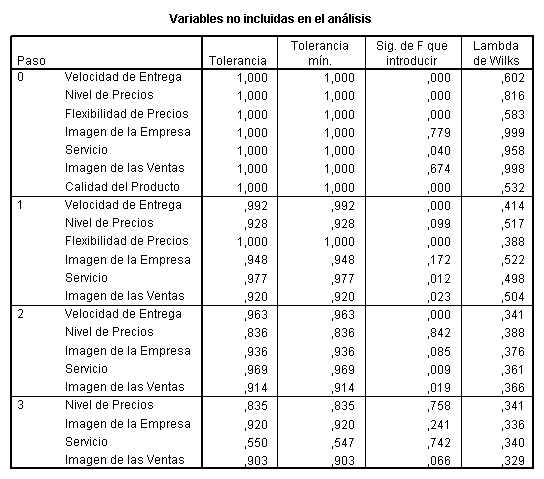
Las tablas subsiguientes muestran los
resultados obtenidos utilizando las variables seleccionadas. Se observa que los
resultados obtenidos son esencialmente los mismos que los obtenidos utilizando
todas las variables.
Resumen de las funciones canónicas discriminantes




4.2 Inconvenientes de
los procedimientos de selección de variables
Conviene
destacar los siguientes (ver Huberty (1989) para más detalles).
1) No
tienen por qué llegar a la solución óptima
2) Utilizan
como criterios de selección, criterios de separación de grupos y no de
clasificación
3) El
nivel de significación global es superior al establecido para entrar y sacar
variables debido a la realización simultánea de varios test de hipótesis.
4. PROCEDIMIENTOS DE CLASIFICACIÓN
Existen varios métodos de clasificación
dependiendo del número de grupos a clasificar (dos o más grupos), de las
hipótesis hechas acerca del comportamiento de las variables en cada grupo
(normalidad conjunta, homocedasticidad) así como del criterio utilizado para
llevar a cabo dicha clasificación.
Uno de los criterios más utilizados es
el criterio Bayes que es el que
expondremos, a continuación, distinguiendo entre el caso de dos y más de dos
grupos, si la discriminación se lleva a cabo bajo hipótesis de normalidad o no
normalidad y/o bajo hipótesis de homo y heterocedasticidad.
4.1 Discriminación de dos poblaciones normales homocedásticas
Suponer que Y
~
Np(mi,S)
i=1,2 en cada uno de los grupos.
Sea y
el valor de las variables de clasificación de una nueva observación cuya
pertenencia a uno de los dos grupos se desconoce.
El criterio Bayes
utiliza el teorema de Bayes para determinar a qué grupo pertenece.
Para ello considera {pi
= P[Gi] i=1,2} las
probabilidades a priori de que la observación considerada pertenezca a cada
grupo. Se suelen tomar pi
= 0.5 i=1,2 si no se dispone de información previa o pi
= ![]() i=1,2 si los tamaños
muestrales de cada grupo reflejan la composición de la población analizada.
i=1,2 si los tamaños
muestrales de cada grupo reflejan la composición de la población analizada.
Aplicando el teorema de Bayes se tiene
que:
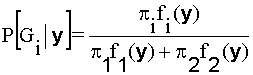 ; i=1,2
; i=1,2
donde
fi(y)
µ
exp[-0.5(y-mi)’S-1(y-mi)] i=1,2 son las funciones de densidad de Y
en cada uno de los grupos.
La observación y
se asignará al grupo G1
si:
P[G1 |
y] > P[G2
| y]
Û
p1f1(y)
> p2f2(y)
Û
Û (y-m1)’S-1(y-m1) < (y-m2)’S-1(y-m2) - log
![]()
Û y’S-1(m2-m1) < 0.5(m1+m2)’S-1(m2-m1)
- log ![]()
Observaciones
1) Si
p1
= p2
el criterio Bayes asignará la observación y
al grupo cuya media, mi,
esté a menor distancia de Mahalanobis la cual viene dada por d(y,mi)
= (y-mi)’S-1(y-mi).
Esta distancia también se utiliza para examinar la existencia de atípicos. Para
ello se utiliza el hecho de que, bajo hipótesis de normalidad, Dobs=![]() ~
~
![]() donde d = (d1,...,dk)'
son las puntuaciones en las k funciones discriminantes de cada individuo y SD
es su matriz de varianzas y covarianzas. Para evaluar si un punto es sospechoso
de ser atípico se calcula el p-valor dado por:
donde d = (d1,...,dk)'
son las puntuaciones en las k funciones discriminantes de cada individuo y SD
es su matriz de varianzas y covarianzas. Para evaluar si un punto es sospechoso
de ser atípico se calcula el p-valor dado por:
![]()
2) El
criterio Bayes utiliza como función de clasificación, la función lineal dada
por y’S-1(m2-m1) y
establece como punto de corte entre los dos grupos 0.5(m1+m2)’S-1(m2-m1)
- log ![]()
3) Geométricamente,
el espacio p-dimensional de los objetos queda dividido en dos regiones
separadas por el hiperplano y’S-1(m2-m1) = 0.5(m1+m2)’S-1(m2-m1)
- log ![]()
4) Si
existe un coste asociado diferente a la asignación incorrecta a cada uno de los
grupos, de forma que la matriz de pérdidas viene dada por:
|
Asignado\Verdadero |
G1 |
G2 |
|
G1 |
0 |
c12 |
|
G2 |
c21 |
0 |
se calculan las
pérdidas esperadas medias a posteriori:
L(Asignar
a G1/y)
= c12P[G2|
y]
L(Asignar
a G2/y)
= c21P[G1|
y]
y
se asigna la observación y
al grupo G1
si:
L(Asignar
a G1/y)
< L(Asignar a G2/y)
Û
Û y’S-1(m2-m1) < 0.5(m1+m2)’S-1(m2-m1)
- log ![]()
4.2 Discriminación de dos
poblaciones normales heterocedásticas
Si Y ~ Np(mi,Si)
i=1,2 en cada uno de los grupos con S1
¹
S2
entonces las funciones de densidad de Y
vendrán dadas por:
fi(y)
µ
|Si|-1/2exp[-0.5(y-mi)’Si-1(y-mi)] i=1,2
y se tendrá que:
P[G1/y]
> P[G2/y]
Û
Û (y-m1)’S1-1(y-m1)
- (y-m2)’S2-1(y-m2)
< log 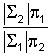
La función discriminante será, por lo
tanto, la forma cuadrática (y-m1)’S1-1(y-m1)
- (y-m2)’S2-1(y-m2)
en lugar de ser una función lineal como en el caso anterior. Coviene hacer
notar, sin embargo, que el criterio lineal especificado anteriormente es más
robusto que el criterio cuadrático a la hipótesis de normalidad y es el que se
suele utilizar habitualmente.
4.3 Discriminación de q grupos
Los criterios vistos con
dos grupos se generalizan a más de dos grupos de forma trivial.
Así, por ejemplo, suponer que Y
~
Np(mi,S)
i=1,…,q en cada uno de los grupos
Las funciones de densidad de Y
vendrán dadas por:
fi(y)
µ
exp[-0.5(y-mi)’S-1(y-mi)] i=1,…,q
El criterio Bayes clasifica la
observación y
en el grupo g si:
P[Gg/y]
= ![]() P[Gk/y] Û
P[Gk/y] Û
Û
y’S-1mg - 0.5mgS-1mg
+ log pg
= ![]() {
y’S-1mk - 0.5mkS-1mk+
log pk}
{
y’S-1mk - 0.5mkS-1mk+
log pk}
Las funciones discriminantes son
lineales y vienen dados por:
y’S-1mg - 0.5mgS-1mg
+ log pg
g
= 1,…,q
Ejemplo 1 (continuación)
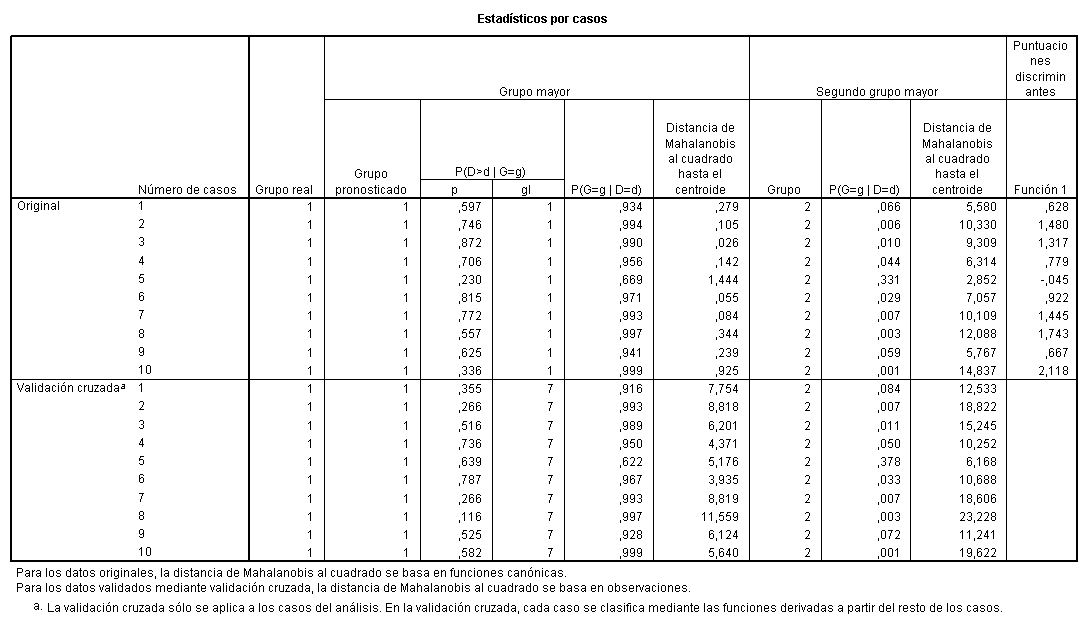
La
siguiente tabla contiene los resultados obtenidos, para 10 clientes de la
empresa, en el proceso de clasificación aplicando el criterio Bayes con
probabilidades a priori iguales para cada grupo y bajo hipótesis de
homocedasticidad y normalidad. SPSS 9.0 (como muchos otros programas) calcula las
probabilidades a posteriori de cada grupo para cada caso, así como la distancia
de Mahalanobis. Así, por ejemplo, para el caso 1, perteneciente al grupo 1, el
grupo pronosticado utilizando todos los casos del análisis es el grupo 1 debido
a que P(G=1/D=d)=0.934 frente a P(G=2/D=d)=0.066. La distancia de Mahalanobis
al centroide de este grupo es igual a 0.279 y el p-valor ![]() =0.597 por lo que
dicho caso no es sospechoso de ser atípico.
=0.597 por lo que
dicho caso no es sospechoso de ser atípico.
Estadísticos de clasificación
4.4 Homocedasticidad
La
homocedasticidad es una hipótesis que se utiliza en algunas de las técnicas
multivariantes (ANOVA, MANOVA, Análisis Discriminante) y se refiere a suponer
la igualdad de las matrices de varianzas y covarianzas de las variables
analizadas en diversos grupos.
El propósito de los test de
homocedasticidad es contrastar la existencia de esta igualdad que, en muchas
ocasiones, va ligada a una falta de normalidad de las variables analizadas.
Para ello se suele utilizar el test M de Box. Este test toma como hipótesis
nula la de homocedasticidad y como alternativa la de heterocedasticidad
(desigualdad de matrices de varianzas y covarianzas), es decir:
Ho:
S1
= … = SG vs
H1:
No todas Sg
son iguales
El
estadístico del test está construido a partir del estadístico:
M = 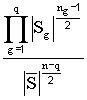
donde
Sg
= ![]() ; g = 1,…,q y
; g = 1,…,q y ![]()
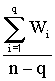
Observaciones
1) La
hipótesis de normalidad es necesaria para los test de significación de las
funciones discriminantes. El efecto de la falta de normalidad sobre la regla de
clasificación es menor. Si no hay normalidad se aconseja utilizar otros
procedimientos como, por ejemplo, la regresión logística
2) La
hipótesis de homocedasticidad afecta a la validez de los test de significación
y de la regla de clasificación. La violación de esta hipótesis puede producir
graves desajustes si hay diferencias grandes entre el tamaño de los grupos y si
el número de variables es elevado
Si hay normalidad conviene utilizar la regla de
clasificación cuadrática especialmente si el tamaño muestral es grande
3)
Una posible solución a los problemas de la falta de normalidad y homocedasticidad
es llevar a cabo transformaciones de las variables.
Las
transformaciones más utilizadas son las de Box-Cox que vienen dadas por (X+C)p
con C, p ctes reales p¹0
y log(X+C) si p = 0. En general si la distribución es muy asimétrica hacia la
derecha se pueden intentar transformaciones del tipo anterior con p < 1 (las
más utilizadas son con p = 0.5 y la transformación logarítmica). Si lo es hacia
la izquierda se aplica la transformación a - X. Si la distribución de los datos
es muy leptocúrtica (curtosis muy grande) se suelen utilizar valores de p< 0
(el más utilizado es p = -1). Si es platicúrtica entonces conviene utilizar
valores de p > 1.
Una forma empirica de
determinar el valor de p más apropiado son los gráficos nivel-dispersión (Spread-versus-level-plot). Dichos gráficos representan en abscisas un estimador
robusto del logaritmo del nivel medio por grupos (en SPSS el logaritmo de la
mediana) y en ordenadas un estimador robusto de la dispersión (en SPSS el
logaritmo del rango intercuartílico) y estiman el coeficiente de regresión b
mediante regresión lineal. A partir de b
es posible deducir cuál es el valor de p más apropiado.
4.5 Discriminación no
paramétrica
Si no hay
normalidad conjunta existen varias opciones posibles:
-
Transformar las variables para
conseguir normalidad
-
Llevar a cabo el análisis con los
rangos
-
Utilizar estimadores no
paramétricos de fi(y)
Si algunas de las variables
clasificadoras no sean cuantitativas. En estos casos se suelen transformar a
cuantitativas. La forma de llevar a cabo este
paso depende del tipo de variable
-
Las variables binarias se
transforman a 0-1
-
Las variables ordinales se
transforman en rangos
Las variables nominales utilizan transformaciones basadas
en sus distribuciones de frecuencias como, por ejemplo, la de Lancaster-Fisher
descrito, por ejemplo, en Huberty (1994), Capítulo 10.
5.- EVALUACIÓN DEL
PROCEDIMIENTO DE CLASIFICACIÓN
Se evaluan tres aspectos del mismo: su
eficiencia, su significación estadística y su significación práctica
5.1 Evaluación de la eficiencia
Para evaluar su eficiencia se construye la tabla de confusión que es una tabla de
frecuencias cruzadas que refleja los resultados de aplicar dicho procedimiento
a los casos observados. Así, en el caso
de la discriminación de dos grupos dicha tabla sería de la forma:
|
|
|
Grupo |
Predicho |
|
|
|
1 |
2 |
|
Grupo |
1 |
n11 |
n12 |
|
Real |
2 |
n21 |
n22 |
donde
nij es el número de casos
pertenecientes al grupo i y para los cuales el mecanismo de clasificación ha
predicho que pertenecen al grupo j. La proporción de bien clasificados vendrá
dada por:
100
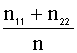 %
%
El proceso de evaluación se puede
llevar a cabo de varias formas. 3 de las más utilizadas son las siguientes:
-
Con los casos utilizados en el
análisis
-
Dividiendo la muestra en dos
partes: una para estimar las funciones discriminantes y otra para evaluarla
-
Utilizando, para cada caso, las
funciones discriminantes estimadas mediante el resto de los casos
El primer procedimiento no es muy aconsejable puesto que
tiende a sobrevalorar el proceso de clasificación. Suele funcionar bien si ming
ng > 5p. El segundo
procedimiento es aconsejable si n es suficientemente grande y funciona
bien si ming
ng > 3p tomando en torno a un 35%
de la muestra para validar. En el resto de los casos se aconseja el tercer
procedimiento. Otros procedimientos para evaluar el mecanismo de predicción
pueden verse en Huberty (1994) capítulo 6.
5.2 Significación estadística
Se
evalúa comparando los resultados obtenidos con los que se obtendrían aplicando
un mecanismo aleatorio. Los dos mecanismos más utilizados son el criterio de aleatoriedad proporcional,
que clasifica de acuerdo a la distribución 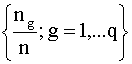 y el de máxima
aleatoriedad que clasifica todas las observaciones asignándolas al grupo de
mayor tamaño.
y el de máxima
aleatoriedad que clasifica todas las observaciones asignándolas al grupo de
mayor tamaño.
Para
comparar los resultados se utilizan estadísticos con distribución
aproximadamente normal bajo la hipótesis de que no existen diferencias. Así, en
el caso de que el criterio utilizado sea el del menanismo aleatorio.
Zg
= 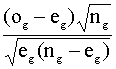
para
evaluar los resultados en cada grupo y
Z
= 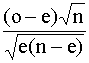
con
para evaluar el proceso globalmente
siendo:
og
= ngg número de
clasificaciones correctas en el grupo g
eg
= ![]() el número esperado de
dichas clasificaciones
el número esperado de
dichas clasificaciones
o
= ![]() número de
clasificaciones correctas
número de
clasificaciones correctas
e
= ![]() el número de clasificaciones correctas esperadas
el número de clasificaciones correctas esperadas
5.3 Significación práctica
Aún cuando un procedimiento sea
significativamente mejor que un mecanismo aleatorio desde un punto estadístico,
no tiene por qué ser mucho mejor desde un punto de vista práctico. Debido a
esto es necesario medir el grado de mejoría de la regla propuesta con respecto a la clasificación debida al azar.
Para ello se utiliza el índice I cuya expresión viene dada
por:
I
= 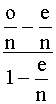 x 100 si se evalúa al proceso globalmente
x 100 si se evalúa al proceso globalmente
Ig
= 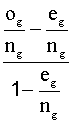 x 100 si se evalúa al proceso en el grupo g
x 100 si se evalúa al proceso en el grupo g
Este índice mide el procentaje de reducción en el error
que resultaría si se utilizara la regla propuesta por el Análisis
Discriminante.
Ejemplo
1 (continuación)
La tabla subsiguiente muestra la tabla de confusión
obtenida utilizando todos los casos del análisis y el procedimiento de
validación cruzada. Se observa, en particular, que el procedimiento de
clasificación ha funcionado correctamente en un 89% = 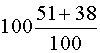 de los casos originales y un 87%=
de los casos originales y un 87%=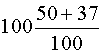 si el procedimiento seguido en la evaluación de la
eficiencia, ha sido el de validación cruzada.
si el procedimiento seguido en la evaluación de la
eficiencia, ha sido el de validación cruzada.
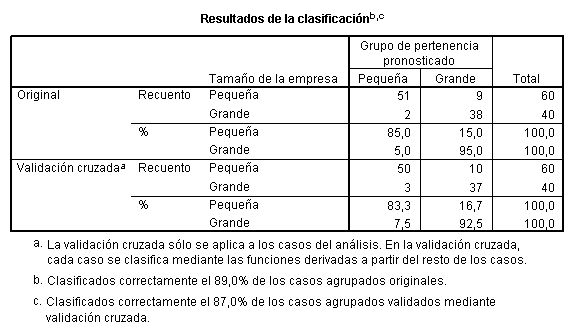
En la siguiente tabla se evalúa la significación
estadística y la significación práctica de los resultados obtenidos comparando
el procedimiento de clasificación con el mecanismo aleatorio proporcional.
|
Grupo |
eg |
Zg |
p-valor |
Ig |
|
Pequeñas |
36 |
3.69 |
0.00 |
41.67 |
|
Grandes |
16 |
6.78 |
0.00 |
12.50 |
|
Global |
52 |
7.01 |
0.00 |
27.08 |
Así, por ejemplo, e1
= 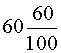 = 36 es el número esperado de éxitos obtenidos en el grupo de
empresas pequeñas mediante el mecanismo aleatorio proporcional y Z1
=
= 36 es el número esperado de éxitos obtenidos en el grupo de
empresas pequeñas mediante el mecanismo aleatorio proporcional y Z1
= 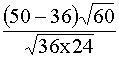 =3.69 y el p-valor es P[Z³3.69]=0.00.
La significación práctica será igual a I1
=
=3.69 y el p-valor es P[Z³3.69]=0.00.
La significación práctica será igual a I1
= 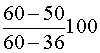 = 41.67 por lo que
nuestro mecanismo mejora al azar en un 41.67% en las empresas pequeñas. Se
observa que todos los resultados son significativos aunque la mejora práctica,
en cada uno de ellos no es excesivamente alta.
= 41.67 por lo que
nuestro mecanismo mejora al azar en un 41.67% en las empresas pequeñas. Se
observa que todos los resultados son significativos aunque la mejora práctica,
en cada uno de ellos no es excesivamente alta.
Resumen
El Análisis Discriminante es una
técnica estadística multivariante con una finalidad doble:
1) Un
fin descriptivo consistente en analizar si existen diferencias entre una serie
de grupos en los que se divide una población, con respecto a un conjunto de
variables y, en caso afirmativo, averiguar a qué se deben
2) Un
fin predictivo consistente en proporcionar procedimientos sistemáticos de
clasificación de nuevas observaciones de origen desconocido en algunos de los
grupos considerados.
Para llevar a cabo un análisis de este tipo se deben los
siguientes pasos:
1) Plantear
el problema a resolver
2) Analizar
si existen diferencias significativas entre los grupos
3) Establecer
el número y composición de las dimensiones de discriminación entre los grupos
analizados
4) Evaluar
los resultados obtenidos desde un punto de vista predictivo analizando la
significación estadística y práctica del procedo de discriminación
Conviene hacer notar, finalmente, que el Análisis Discriminante
no es la única técnica estadística implicada en el proceso de clasificación de
observaciones en grupos previamente fijados por el analista. Otra alternativa
interesante viene dada por los modelos de regresión con variable dependiente
cualitativa (de los que el Análisis Discriminante podría considerarse un caso
particular) como son, por ejemplo, los modelos de regresión logit y probit que
son desarrollados en otras páginas Web de este portal.
Bibliografía
Como libro de consulta dedicado
exclusivamente al Análisis Discriminante y con un montón de referencias
adicionales recomiendo:
HUBERTY, C.J. (1994). Applied Discriminant Analysis. Wiley.
Interscience
Libros de Análisis Multivariantes que
contienen buenos capítulos acerca del Análisis Discriminante.
Desde un punto de vista más práctico:
AFIFI, A.A. and CLARK, V. (1996) Computer-Aided Multivariate Analysis. Third Edition. Texts in
Statistical Science. Chapman and Hall.
EVERITT, B. And GRAHAM, D. (1991). Applied Multivariate Data Analysis. Arnold.
HAIR, J., ANDERSON, R., TATHAM, R. y BLACK, W. (1999).
Análisis
Multivariante. 5ª Edición. Prentice Hall.
SHARMA, S. (1998). Applied Multivariate Techiques. John
Wiley and Sons.
URIEL, E.
(1995). Análisis de Datos: Series
temporales y Análisis Multivariante. Colección Plan Nuevo. Editorial AC.
Desde un punto de vista más
matemático:
JOBSON, J.D. (1992) Applied
Multivariate Data Analysis. Volume II: Categorical and Multivariate Methods.
Springer-Verlag.
MARDIA, K.V., KENT, J.T. y
BIBBY, J.M. (1994). Multivariate
Analysis. Academic Press.
Enfocados hacia SPSS:
FERRAN, M. (1997). SPSS
para WINDOWS. Programación
y Análisis Estadístico. Mc.Graw
Hill.
VISAUTA,
B. (1998) Análisis Estadístico con SPSS
para WINDOWS (Vol II. Análisis Multivariante). Mc-Graw Hill.
Otros trabajos
citados en la lección.
HUBERTY, C.J. (1989). Problems with stepwise methods:
Better alternatives. In B. Thompson (Ed.). Advances
in social science methodology (Vol. 1). pp. 43-70. Greenwich, CT: JAI
Press.
