Otro paso importante
que debemos dar ahora antes de continuar es la asignación
de los nombres siguientes a los rangos que indicamos: (nótese que
el número de celdas que componen cada rango es 96, ya
que el número máximo de cuotas posibles para este
ejercicio es ése, correspondiente a 8 años y por
mensualidades):
|
Rango
de celdas |
Nombre
asignado |
|
B18:B113 |
npagos |
|
C18:C113 |
fechas |
|
D18:D113 |
cuotamort |
|
E18:E113 |
cuotaint |
|
F18:F113 |
terminoamort |
|
G18:G113 |
ppalamort |
|
H18:H113 |
deudaviva |
Para obtener la fecha
del último término amortizativo, celda J7, hemos empleado la
siguiente función:
=SI(J4="" ; "" ; MAX(Fechas
))
En donde Fechas
es el rango (C18:C113) correspondiente a la columna C (Fecha del Pago) del cuadro de amortización del
préstamo. La función MAX proporciona el máximo valor de un rango.
Para obtener los Intereses,
celda J8, hemos empleado la
siguiente función:
=SI(J4="" ; "" ; E114
)
En donde E114 es la suma de los
intereses de la columna correspondiente del cuadro amortizativo.
Defintivamente en estos
momentos de construcción del modelo tendríamos
únicamente el siguiente aspecto:

A continuación
procedemos a completar el CUADRO DE AMORTIZACIÓN del Préstamo;
va a tener la siguiente estructura:

Concretamente va a
estar ubicado y estructurado del siguiente modo: (El ejemplo
está hecho para 16 trimestres)
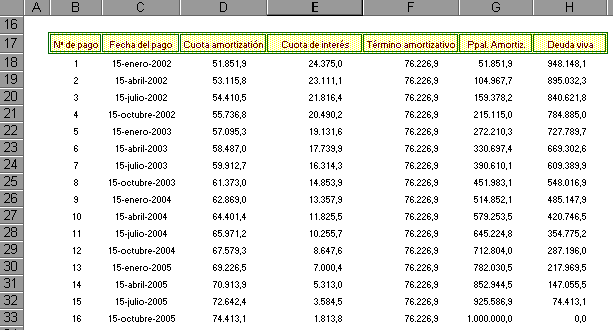
Las celdas que vamos
a analizar para ver sus fórmulas son estas: (Quizá
por ser la más compleja, dejaremos para el final la columna
C "Fecha del Pago")

|
B18 |
=SI( J4="" ; "" ; 1
) |
|
B19 |
=SI( B18="" ; "" ; SI( 1+B18<=n*fraccion ; 1+B18 ; "" ) ) |
El
efecto que se quiere conseguir es que ponga el número
de pago siempre que exista, en otro caso que no coloque nada.
|
D18 |
=SI( B18="" ; "" ; F18-E18
) |
|
D19 |
=SI( B19="" ; "" ; F19-E19 ) |
Podremos
visualizar alguna cuota de amortización siempre
que exista algún dato en las celdas de la columna previa
B. Si nos fijamos es
igual al Término amortizativo menos la cuota de interés.
|
E18 |
=SI( B18="" ; "" ; (tipo/fraccion)*montante
) |
|
E19 |
=SI( B19="" ; "" ; (tipo/fraccion)*H18 ) |
Podremos
visualizar alguna cuota de interés siempre que
exista algún dato en las celdas de la columna previa B. En esta ocasión en E18, tenemos el tipo fraccionado
por el montante que se encontraba en la celda E4. Por contra, en la
celda E19, tenemos algo muy
similar, pero en esta ocasión el importe que se toma es
de la columna Deuda Viva, ya que el interés debe calcularse
sobre la cantidad de principal pendiente de amortizar.
|
F18 |
=SI( B18="" ; "" ; J$4
) |
|
F19 |
=SI( B19="" ; "" ; J$4
) |
Podremos
visualizar el término amortizativo siempre que
exista algún dato en las celdas de la columna previa B. En esta ocasión en toda la
columna la fórmula colocada coincide, puesto que el término
amortizativo no varía, incluso si prestamos atención
la celda J4, está puesta
como J$4 (referencia relativa),
de forma que cuando se copie hacia abajo la fila no varíe
y se refiera siempre a la celda J4.
|
G18 |
=SI( B18="" ; "" ; D18
) |
|
G19 |
=SI( B19="" ; "" ; D19+G18
) |
Podremos
visualizar el Principal amortizado siempre que exista
algún dato en las celdas de la columna previa B. En esta ocasión las fórmulas
de las celdas G18 y G19 varían prácticamente
en nada, puesto que en el primer pago lo que se ha amortizado
es simplemente la parte de principal de dicho pago (que tenemos
en la columna D) ... en cambio, en
el segundo si que comenzamos a "acumular" principal,
puesto que tenemos la parte amortizada del pago actual más
lo que llevemos acumulado hasta la fecha.
|
H18 |
=SI( B18="" ; "" ; montante-G18
) |
|
H19 |
=SI( B19="" ; "" ; montante-G19
) |
Podremos
visualizar la Deuda viva (Capital pendiente de amortizar)
siempre que exista algún dato en las celdas de la columna
previa B. En esta ocasión
las fórmulas son similares en toda la columna H, es decir lo que quedará pendiente
de amortizar en todo momento de principal es el montante inicial
(J4) menos la parte de
principal amortizada y acumulada hasta la fecha de dicho pago
(columna G).
|
C18 |
=SI( B18="" ; "" ; E7
) |
|
C19 |
=SI( B19="" ; "" ; FECHA(AÑO(C18) ; MES(C18)+(12/fraccion) ; MIN( DIA($C$18) ; DIA( FECHA( AÑO(C18) ; MES(C18)+(12/fraccion)+1 ; 0 ) )
) ) ) |
Hemos
empleado esta función por el hecho de que todos los meses
no tienen igual número de días.
Podremos
visualizar la Fecha del pago correspondiente siempre que
exista algún dato en las celdas de la columna previa B. Quizá en este caso haya que
comentar la celda C19. La función
FECHA me proporciona un
número de Serie (número serial) de la fecha
a la que haga referencia (el lector podrá visualizar dichos
números seriales simplemente dando el formato número
Estándar a la fecha en cuestión), por ejemplo:
|
Fecha |
Número
serial |
|
1-Enero-1900 |
1 |
|
1-Enero-1901 |
367 |
|
1-Enero-2000 |
36.526 |
|
1-Agosto-2000 |
36.739 |
|
7-Enero-2002 |
37.263 |
Si nos fijamos, por
diferencia de los números seriales obtendríamos
el Número
de DÍAS entre 2 fechas...
...Volviendo al ejercicio
que estamos desarrollando, lo que le pedimos en C19 a fin de cuentas es
simplemente una Fecha, cuyo año es inicialmente el de la fecha del
pago previo [AÑO(C18)] (en nuestro ejercicio es el año 2002), el mes es el mes previo más
un número de meses equivalente a (12/fraccion), es decir,
si fraccion vale 12 añadiría un mes, si fracción
vale 3 añadiría un cuatrimestre, etc... [MES(C18)+(12/fraccion)] (en nuestro ejercicio
es el mes de abril que es el trimestre siguiente) y el día será el menor
de 2 posibilidades:
a.- el número de día de
la fecha inicial del Préstamo ($C$18). [DIA($C$18)] (en nuestro caso el día 15).
b.- [DIA( FECHA( AÑO(C18) ; MES(C18)+(12/fraccion)+1 ; 0 )] (en nuestro caso también
sale el día 15). Es de gran importancia que comentemos
que en este caso lo que se selecciona es el día 0 del mes siguiente al que indicamos
con +(12/fraccion), que sería del mes de mayo,
lo cual nos proporcionaría el último día
del mes anterior (abril) en caso de que fuera necesario...
esto es muy importante -insistimos- por el hecho de que los meses
tienen distinto número de días.

