|
Lección Estadística |
Modelos de regresión con respuesta cualitativa: regresión logística
|
||
|
Citar como: Salvador Figueras, M (2001):
"Modelos de regresión con respuesta cualitativa: regresión
logística", [en línea] 5campus.com, Estadística
<http://www.5campus.com/leccion/logis> [y añadir fecha consulta] |
||
1.- MODELOS DE REGRESION CON RESPUESTA DICOTÓMICA
1.1 Planteamiento del problema
Sea Y una variable dependiente binaria tomando dos valores posibles que
etiquetaremos como 0 y 1.
Sean X1,…,Xk un conjunto de
variables independientes observadas con el fin de explicar y/o predecir el
valor de Y.
Nuestro objetivo consiste en
determinar P[Y=1/X1,...,Xk] ( y por lo tanto P[Y=0/X1,...,Xk] = 1- P[Y=1/X1,...,Xk]).
Para ello construimos
un modelo de la forma:
P[Y=1/X1,...,Xk] = p(X1,…,Xk ;b)
donde p(X1,…,Xk ;b): Rk ® [0,1] es una función que recibe el nombre de función de enlace cuyo valor depende de un vector de parámetros b = (b1,...,bk)'.
1.2. Función de verosimilitud
Con
el fin de estimar b y analizar el
comportamiento del modelo considerado observamos una muestra aleatoria simple
de tamaño n dada por {(xi’,yi);i=1,…,n} donde xi = (xi1,…,xik)’ es el valor de las variables independientes e yiÎ{0,1} es el valor observado de Y en el i-ésimo elemento de la muestra.
Utilizando el hecho de que
Y/(X1,...,Xk) ~ Bi(1, p(X1,…,Xk ;b)), la función de verosimilitud vendrá dada por:
L(b|(x1’,y1),…,(xn’,yn)) = 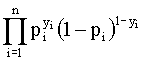
donde pi = p(xi’;b) = p(xi1,…,xik;b); i=1,...,n.
Ejemplos
a) Modelo lineal
p(X1,…,Xk ;b) = 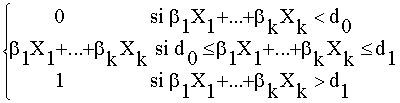
con do, d1 constantes.
b) Modelo probit
p(X1,…,Xk ;b) = F(b1X1 + … + bkXk)
siendo F la función de distribución
de una normal estándar.
c) Modelo logit o modelo de regresión logística binaria
p(X1,…,Xk ;b) = G(b1X1 + … + bkXk)
donde G(x) = ![]() es la función de
distribución de la distribución logística.
es la función de
distribución de la distribución logística.
2. MODELO DE REGRESION LOGISTICA BINARIA
En
este caso se verifica que:
log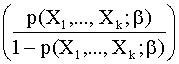 = bo + b1X1 + … + bkXk
= bo + b1X1 + … + bkXk
donde hemos tomado como primera variable explicativa
a la variable constante que vale 1.
La expresión 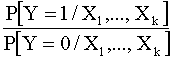 =
=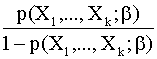 se conoce con el nombre de ratio de riesgo el cual del mundo de la
medicina en el que la variable Y indica, habitualmente, la presencia de una
determinada enfermedad objeto de estudio.
se conoce con el nombre de ratio de riesgo el cual del mundo de la
medicina en el que la variable Y indica, habitualmente, la presencia de una
determinada enfermedad objeto de estudio.
2.1 Función de Verosimilitud
Teniendo en cuenta
que, en este caso,
p(X1,...,Xk;b) = 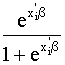
la función de verosimilitud viene dada por:
L(b|(x1’,y1),…,(xn’,yn)) = ![]()
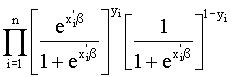
3. INFERENCIA ESTADÍSTICA EN
UN MODELO DE REGRESIÓN LOGÍSTICA BINARIA
3.1 Estimación de los parámetros del modelo
El
vector de parámetros b se estima mediante el
método de máxima verosimilitud y existen dos formas de calcularla: la estimación incondicional y la estimación
condicional.
La estimación incondicional maximiza la función de verosimilitud
anterior y resuelve las ecuaciones:
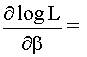
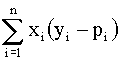 =0
=0
donde
pi = p(xi;b) i=1,…,n,
mediante métodos iterativos.
La estimación condicional maximiza la función de verosimilitud condicional dada por:
LC(b|(x1’,y1),…,(xn’,yn)) = ![]()
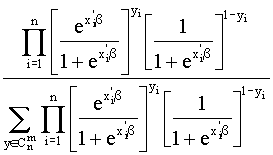
donde y=(y1,...,yn)' y ![]() es el conjunto de
todos los vectores y tales que y1+...+yn es igual al número de veces que Y=1 en la muestra observada.
es el conjunto de
todos los vectores y tales que y1+...+yn es igual al número de veces que Y=1 en la muestra observada.
La estimación
condicional es insesgada, cosa que no ocurre con la estimación incondicional, y
es recomendable utilizarla si el número de parámetros a estimar es muy grande.
En otro caso ambas estimaciones son equivalentes.
3.2 Selección de modelos
El problema es seleccionar de entre
las variables explicativas X1,…,Xk las mejores para explicar la variable Y. Para ello es necesario establecer
el criterio de comparación de modelos y el algoritmo de selección.
3.2.1 Criterios de comparación de modelos
Se utilizan los test
de razón de verosimilitudes (LR), de los multiplicadores de Lagrange (LM) o el
test de Wald (W).
Los tres criterios se
utililizan para llevar a cabo un contraste entre modelos anidados M1 Í M2. Los estadísticos del test vienen dados por las siguientes
expresiones:
LR = ![]()
LM = 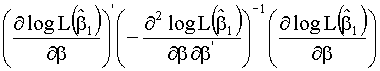
W=![]()
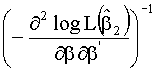
![]()
donde L es la función de verosimilitud del modelo M2 y donde ![]() i=1,2 son los
estimadores máximo-verosimiles de los vectores de parámetros de los modelos M1 y M2.
i=1,2 son los
estimadores máximo-verosimiles de los vectores de parámetros de los modelos M1 y M2.
Los tres contrastes son asintóticamente equivalentes si es cierto el modelo M1 , y su distribución asintótica es ![]() donde q es la
diferencia entre el número de parámetros de M1 y M2.
donde q es la
diferencia entre el número de parámetros de M1 y M2.
3.2.2 Algoritmos de selección de modelos
Existen,
esencialmente, dos clases de algoritmos para llevar a cabo la selección: los métodos de selección hacia delante y los
de eliminación hacia atrás.
3.2.2.1 Algoritmos de selección de variables hacia
adelante
Comienzan con el modelo que tiene
como única variable explicativa el término constante bo. En cada paso del algoritmo entra en la ecuación del modelo aquella
variable con el menor p-valor calculado utilizando uno de los tres criterios
expuestos en 3.2.1. Así mismo se eliminan de la ecuación del modelo aquellas
variables con un valor de dicho estadístico no significativo.
3.2.2.2. Algoritmos de eliminación de variables
hacia atrás
Comienza con el modelo que
tiene todas las variables en la ecuación de regresión. En cada paso elimina de
la ecuación del modelo aquellas variables con un coeficiente bi que no es significativamente distinto de 0 utilizando alguno de los
criterios expuestos en 3.2.1.
3.3 Bondad de ajuste del modelo
Se
utilizan dos tipos de contrastes: los contrastes que analizan la bondad de
ajuste desde un punto de vista global y los que la analizan caso por caso.
3.3.1. Constrastes de bondad de ajuste global
Se utilizan, entre otros, el
índice de bondad de ajuste de Hosmer-Lemeshow, el estadístico desviación y el
contraste de bondad de ajuste de Hosmer-Lemeshow
El índice
de bondad de ajuste de Hosmer-Lemeshow viene dado por:
Z2 = 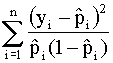
donde ![]() i=1,...,n. La
distribución asintótica de Z2 es
i=1,...,n. La
distribución asintótica de Z2 es ![]() si el modelo ajustado es
cierto.
si el modelo ajustado es
cierto.
El estadístico
desviación viene dado por:
D = 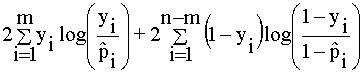
donde m = número de observaciones con yi = 1. La distribución
asintótica de D es ![]() si el modelo ajustado es
cierto.
si el modelo ajustado es
cierto.
3.3.1.2 Contraste de bondad de ajuste de
Hosmer-Lemeshow
Este
contraste evalúa la bondad de ajuste del modelo construyendo una tabla de
contingencia a la que aplica un contraste tipo c2. Para ello calcula los deciles de las probabilidades estimadas {![]() ; i=1,...,n} , D1,...,D9 y divide los datos observados en 10 categorías dadas por
; i=1,...,n} , D1,...,D9 y divide los datos observados en 10 categorías dadas por
Aj = {iÎ{1,...,n} | ![]() Î [Dj-1,Dj)}; j=1,...,10
Î [Dj-1,Dj)}; j=1,...,10
donde Do = 0, D10 = 1.
Sean:
nj = número de casos en Aj ; j=1,...,10
oj = número de yi = 1 en Aj; j=1,...,10
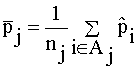 ; j=1,...,10
; j=1,...,10
El estadístico del contraste viene dado por:
T = 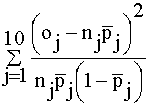
y el p-valor del contraste es P![]()
3.3.2
Diagnósticos del modelo
Evalúan la bondad de
ajuste caso por caso mediante el análisis de los resíduos del modelo y de su
influencia en la estimación del vector de parámetros del mismo.
3.3.2.1. Resíduos del modelo
Los
resíduos más utilizados son los siguientes:
- Resíduos
estandarizados
zi = 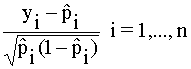
- Resíduos
studentizados:
sti = 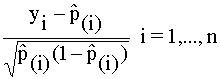
- Resíduos
desviación
di = 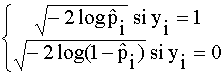 i=1,…,n
i=1,…,n
donde ![]() es la estimación de pi obtenida eliminando la observación i de la
muestra. Todos estos se distribuyen aproximadamente, según una N(0,1), si el
modelo ajustado es cierto.
es la estimación de pi obtenida eliminando la observación i de la
muestra. Todos estos se distribuyen aproximadamente, según una N(0,1), si el
modelo ajustado es cierto.
3.3.2.2. Medidas de
influencia
Cuantifican la
influencia que cada observación ejerce sobre la estimación del vector de
parámetros o sobre las predicciones hechas a partir del mismo de forma que,
cuanto más grande son, mayor es la influencia que ejerce una observación en la
estimación del modelo
- Medida de Apalancamiento
(Leverage)
Se utiliza para detectar observaciones que tienen un
gran impacto en los valores predichos por el modelo
Se calcula a partir de la matriz H = W1/2X(X’WX)-1X’ W1/2 donde W = diag![]() .
.
El apalancamiento para
la observación i-ésima viene dado por el elemento i-ésimo de la diagonal
principal de H, hii, y toma valores entre 0 y 1 con un valor medio de p/n.
Las dos medidas siguientes miden el impacto que
tiene una observación en la estimación de b.
- Distancia de Cook: mide la influencia en la
estimación de b
COOKi = 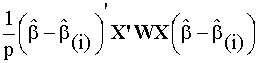
-DFBETA: influencia en la estimación de una componente de b, b1
Dfbeta1i = 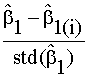
donde ![]() y
y ![]() denotan las
estimaciones MLE de b y b1, eliminando la i-ésima observación
de la muestra y std(
denotan las
estimaciones MLE de b y b1, eliminando la i-ésima observación
de la muestra y std(![]() ) el error estándar en la estimación de b1.
) el error estándar en la estimación de b1.
4. INTERPRETACION DE LOS RESULTADOS
La interpretación de
los resultados obtenidos se realiza a partir de la interpretación de los
coeficientes del modelo. Para ello basta tener en cuenta que si el modelo
ajustado es cierto, entonces se verifica que:
log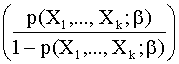 = bo + b1X1 + … + bkXk
= bo + b1X1 + … + bkXk
de donde se sigue que el
ratio del riesgo vendrá dado por:
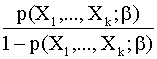 =
= ![]()
y, de aquí que:
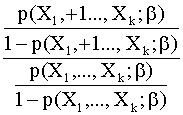 =
= ![]()
Por
lo tanto, ![]() es el factor de
cambio en el ratio de riesgo si el valor de la variable X1 cambia en una unidad. Así, si b1 > 0 (resp. < 0 ) el factor será mayor que 1 y p(X1,…,Xk ;b) aumentará (resp. disminuirá). Si b1 = 0 la variable X1 no ejerce ningún efecto sobre Y.
es el factor de
cambio en el ratio de riesgo si el valor de la variable X1 cambia en una unidad. Así, si b1 > 0 (resp. < 0 ) el factor será mayor que 1 y p(X1,…,Xk ;b) aumentará (resp. disminuirá). Si b1 = 0 la variable X1 no ejerce ningún efecto sobre Y.
bo es un ajuste de escala. Su mejor interpretación se obtiene calculando
el valor de p(X1,…,Xk ;b) en los valores medios de X1,…,Xk y usar como variables
explicativas sus valores estandarizados.
4.1 Variables
explicativas categóricas
Si una de las
variables explicativas es categórica, con c valores posibles, se crean c-1
variables dicotómicas como variables explicativas. Estas variables se pueden
construir de diversas formas y según la forma utilizada cambia la
interpretación de sus coeficientes bi que, en general, cuantifican el efecto de un valor de dichas variables
con respecto a un valor de referencia
Ejemplos
Suponer
que k=1 y X1 es categórica con c = 3.
Dos
formas posibles de codificarla son:
a)
Codificación
tipo indicador con referencia la última categoría de X1.
Consiste en crear las variables Ind1 e Ind2 dadas por:
|
X1 |
Ind1 |
Ind2 |
|
1 |
1 |
0 |
|
2 |
0 |
1 |
|
3 |
0 |
0 |
En este caso la ecuación del
modelo ajustado viene dada por:
log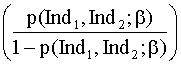 = bo + b1Ind1 + b2Ind2
= bo + b1Ind1 + b2Ind2
Sea pi = P[Y=1/X1=i]; i=1,2,3. Se tiene que:
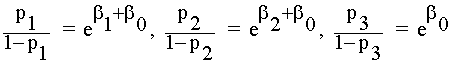
Se
sigue que:
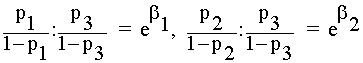
Por
lo tanto, ![]() i=1,2 compara los
ratio de riesgo correspondientes X1 = 1,2 frente al de la categoría de referencia X1 = 3.
i=1,2 compara los
ratio de riesgo correspondientes X1 = 1,2 frente al de la categoría de referencia X1 = 3.
2) Codificación
desviación con referencia la última categoría de X1
Consiste en crear las
variables Desv1 y Desv2 dadas por:
|
X1 |
Desv1 |
Desv2 |
|
1 |
1 |
0 |
|
2 |
0 |
1 |
|
3 |
-1 |
-1 |
En este caso la ecuación del
modelo ajustado viene dada por:
log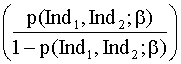 = bo + b1Desv1 + b2Desv2
= bo + b1Desv1 + b2Desv2
y se tiene que:
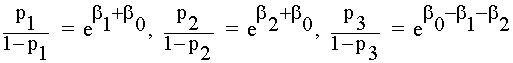
Se
tiene que 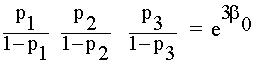
Por
lo tanto, ![]() i=1,2 compara los
ratio de riesgo correspondientes X1 = 1,2 frente a los de una categoría media con un ratio de riesgo que
viene dado por:
i=1,2 compara los
ratio de riesgo correspondientes X1 = 1,2 frente a los de una categoría media con un ratio de riesgo que
viene dado por:
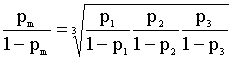
y ![]() lo compara con el
ratio de riesgo de X1 = 3.
lo compara con el
ratio de riesgo de X1 = 3.
5. ANALISIS DISCRIMINANTE PREDICTIVO CON REGRESION
LOGÍSTICA BINARIA
En
este caso el número de grupos considerados por el analista es igual a 2 y
vienen indicados por la variable Y. La asignación a cada grupo se realiza
utilizando el valor estimado ![]() de la probabilidad pi , estableciendo
un punto de corte, cÎ(0,1), tal que,
si
de la probabilidad pi , estableciendo
un punto de corte, cÎ(0,1), tal que,
si ![]() > c,
la observación i-ésima se clasifica en el grupo Y=1 y, en caso contrario se
clasifica en el grupo Y=0. Habitualmente se toma c=0.5.
> c,
la observación i-ésima se clasifica en el grupo Y=1 y, en caso contrario se
clasifica en el grupo Y=0. Habitualmente se toma c=0.5.
Utilizando este
procedimiento se construyen las tablas de clasificación:
|
Observado/Predicho |
Y = 0 |
Y = 1 |
|
Y=0 |
n00 |
n01 |
|
Y=1 |
n10 |
n11 |
El
porcentaje de observaciones bien clasificadas vendrá dado por:
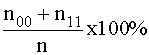
Al
igual que en el Análisis Discriminante clásico, se pueden utilizar diversas
formas para evaluar la capacidad clasificatoria del modelo ajustado tanto desde
un punta estadístico como práctico. Cómo hacerlo se describe con más detalle en
la
lección sobre Análisis Discriminante.
Ejemplo
En
este ejemplo se ilustran algunos de los pasos anteriores mediante un aplicación
habitual de los modelos de regresión logística binaria: el Análisis
Discriminante de dos grupos. Los datos se han tomado del libro de Hair et al.
(1995) y en la lección sobre Análisis
Discriminante se analiza este mismo
ejemplo aplicando técnicas de Análisis Discriminante.
Una empresa está
interesada en analizar la opinión de sus clientes con respecto a su labor
comercial y de gestión. Para ello realiza una encuesta a una muestra de 100 de
ellos en las que le pide que valoren su labor en los siguientes aspectos, haciendo
una valoración entre 0 y 10: Velocidad de Entrega (VENTREGA), Nivel de Precios
(NIVPREC), Flexibilidad de Precios (FLEXPREC), Imagen de la Empresa (IMGEMPR),
Servicio (SERVICIO), Imagen de Ventas (IMGVENTA) y Calidad de Producto
(CALIDAD).
Además, tiene clasificados a sus clientes en dos
grupos de acuerdo al tamaño de la empresa en la que trabajan: Empresas Pequeñas
(TAMAÑO=1) y Empresas Grandes (TAMAÑO=2).
El número de clientes pertenecientes a empresas pequeñas es igual a 60 y
el de empresas grandes es igual a 40.
El objetivo del estudio es analizar si existen
diferencias en cuanto a la percepción de su labor empresarial entre los
clientes de un grupo y del otro y, en caso de que existan, analizar en qué
sentido se dan dichas diferencias. Para ello planteamos el problema como uno de
regresión cuya variable dependiente es TAMAÑO y las variables independientes
son las variables clasificadoras.
- Selección de variables
Aplicamos los
algoritmos de selección de variables hacia delante y eliminación hacia atrás
implementados en el paquete estadístico SPSS 9.0 tomando como criterio de
entrada un p-valor igual a 0.05 y como criterio de salida un p-valor igual a
0.10. En la tabla subsiguiente se muestran los resultados obtenidos:
Tabla I
|
Algoritmo de Selección |
Variables seleccionadas |
-2log L |
% bien clasificados |
|
Hacia delante |
VENTREGA, FLEXPREC, IMGVENTAS, CALIDAD |
27.706 |
96% |
|
Eliminación hacia atrás |
VENTREGA, FLEXPREC, IMGEMPR, IMGVENTAS, CALIDAD |
24.984 |
97% |
|
Todas las variables |
|
24.486 |
96% |
Se observa que los algoritmos de selección hacia delante seleccionan
las variables Velocidad de Entrega, Flexibilidad de Precios, Imagen de Ventas y
Calidad del Producto. Los algoritmos de selección hacia detrás añaden, además,
la variable Imagen de la Empresa. Los modelos elegidos no muestran diferencias
significativas a un nivel del 5% y el porcentaje de bien clasificados
intra-muestral es similar. Nos quedamos, por lo tanto, con el modelo más
parsimonioso.
-
Bondad de ajuste
La siguiente tabla muestra los resultados de aplicar
el test de bondad de ajuste de Hosmer-Lemeshow. Se observa que la bondad de
ajuste global es buena.
---------- Hosmer
and Lemeshow Goodness-of-Fit Test-----------
TAMAÑO = Pequeña TAMAÑO = Grande
Group Observed
Expected Observed Expected Total
1
10,000 10,000 ,000 ,000 10,000
2
10,000 9,997 ,000 ,003 10,000
3
10,000 9,988 ,000 ,012 10,000
4
10,000 9,954 ,000 ,046 10,000
5
10,000 9,734 ,000 ,266 10,000
6
8,000 7,748 2,000 2,252 10,000
7
2,000 1,942 8,000 8,058 10,000
8
,000 ,513 10,000 9,487 10,000
9
,000 ,120 10,000 9,880 10,000
10
,000 ,004 10,000 9,996 10,000
Chi-Square df Significance
Goodness-of-fit
test 1,0394 8
,9980
--------------------------------------------------------------
-
Análisis de resíduos y
puntos influyentes
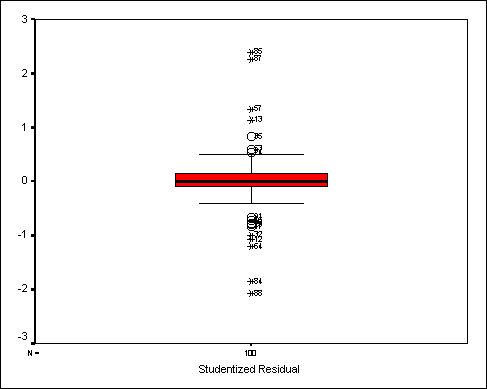
El siguiente boxplot muestra los resíduos
estudentizados. No existe ningún resíduo cuyo valor absoluto sea mayor que 3
aunque sí existen 4 casos con resíduos mayores que 2. Podemos, por tanto, decir, que el ajuste es correcto.
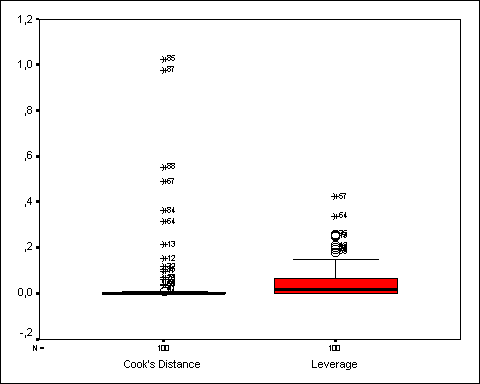
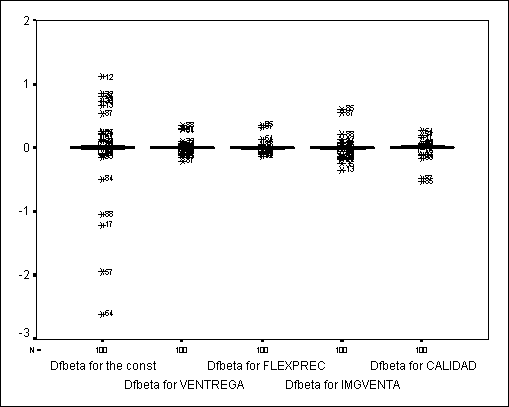
Los diagramas posteriores analizan la existencia de
puntos influyentes. No se observa ningún caso que tenga un efecto significativo
sobre las estimaciones de los parámetros del modelo
-
Análisis del comportamiento
predictivo extramuestral
La siguiente tabla muestra la tabla de clasificación tomando el 35% de
la muestra para validar. El porcentaje de bien clasificados es del 94.59% y el
modelo mejora significativamente los resultados obtenidos con un Análisis
Discriminante clásico.
Predicted
Pequeña
Grande Percent Correct
P ó G
Observed ôòòòòòòòòôòòòòòòòòô
Pequeña P ó 24
ó
1 ó 96,00%
ôòòòòòòòòôòòòòòòòòô
Grande G ó 1
ó
11 ó 91,67%
ôòòòòòòòòôòòòòòòòòô
Overall 94,59%
-
Estimación de los parámetros
La siguiente tabla muestra las estimaciones de los
parámetros del modelo así como el resultado de aplicar el test de Wald a cada
uno de ellos. Todos ellos son significativos para un nivel de significación del
5%. Todas las variables seleccionadas tienen un efecto negativo sobre el ratio
de riesgo y, por lo tanto, sobre la probabilidad de que una empresa tenga un
tamaño grande, con la única excepción de la Calidad del Producto.
La última columna muestra el valor de eb que cuantifica
en cuánto se incrementaría el ratio de riesgo si cada variable se incrementara
en una unidad. Se observa que, para la Velocidad de Entrega, Flexibilidad de
Precios e Imagen de Ventas un incremento de una unidad en la valoración en
estos aspectos, disminuye el factor de riesgo en un 72.74%, 75.77% y 90.44%,
respectivamente. Por el contario, si aumenta la valoración en Calidad de
Producto, se incrementa el riesgo en un 124.128%
Podemos, por tanto, concluir, que existen
diferencias entre las empresas grandes y pequeñas mostrando las primeras una
tendencia a valorar mejor la labor de nuestra empresa en la calidad del
producto ofrecido; por el contrario, las empresas pequeñas muestran una
tendencia a valorar mejor aspectos como la velocidad de entrega, la
flexibilidad de precios y la imagen de ventas.
------------- Variables in the Equation -----------------------
Variable B S.E. Wald df
Sig R Exp(B)
VENTREGA -1,2996 ,6473 4,0304
1 ,0447 -,1228
,2726
FLEXPREC -1,4176 ,4781 8,7903
1 ,0030 -,2246
,2423
IMGVENTA -2,3480 ,9548 6,0475
1 ,0139 -,1734
,0956
CALIDAD 2,5962 ,7393 12,3328
1 ,0004 ,2771
13,4128
Constant 1,7331 4,3887 ,1559
1 ,6929
6. OBSERVACIONES MULTIPLES
Si
las variables explicativas X1, ..., Xk son categóricas, se tiene una tabla de contingencia k-dimensional y
pueden aparecer medidas repetidas. En este caso se cuenta, para cada una de las
celdas de dicha tabla el número de observaciones ni que hay en la misma así como
el número de casos, mi, en los cuales Y=1.
En
este caso la función de verosimilitud del modelo de regresión vendrá dada por:
L(b|(x1’,y1),…,(xn’,yn)) = 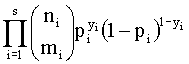
donde s es el número de celdas de la tabla de
contingencia y pi = p(xi;b); i=1,...,s.
Los estadísticos de bondad
de ajuste del modelo así como los diagnósticos del mismo se calculan de acuerdo
a esta nueva situación. Así, por ejemplo, los resíduos estandarizados y los
resíduos desviación vienen dados por:
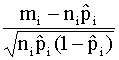 y
y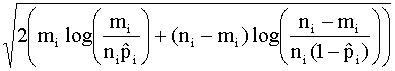
respectivamente.
También
se puede modelizar efectos interacción entre las distintas variables. Para
detalles ver (http://www2.chass.ncsu.edu/garson/pa765/logit.htm).
7. MODELO
LOGÍSTICO MULTINOMIAL
En
este caso se supone que la variable dependiente Y tiene más de dos categorías y
utiliza como distribución subyacente la distribución multinomial.
Sea g el número de categorías de Y. El modelo logístico
multinomial supone que:
P[Y=i/x] =
pj = 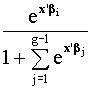 i=1,...,g-1
i=1,...,g-1
P[Y=g/x] = pg = 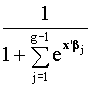
Observar
que:
![]() =
=![]() si r,s¹g y
si r,s¹g y ![]() =
=![]()
por lo que el ratio de dos probabilidades de cada
categoría es independiente de los parámetros del resto de las categorías. Esta
propiedad se conoce con el nombre de independencia
de alternativas irrelevantes
7.1 Inferencia
en un modelo logit multinomial
La
función de verosimilitud viene dada por:
L((b1,...,bg-1)|(x1’,y1),…,(xn’,yn)) = 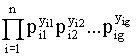
donde yi = (yi1,...,yig)' i=1,...,n de forma que yij = 1 si Y=j para la
observación i-ésima y pij = P[Y=j/xi;(b1,...,bg-1)].
La
estimación de los parámetros se lleva a cabo por máxima verosimilitud y la
selección y el estudio bondad de ajuste del modelo es realiza de forma similar
al modelo de regresión logística binaria.
Por
último, de forma análoga al caso binario, es posible llevar a cabo un Análisis
Discriminante Predictivo. En este caso cada observación se asignaría al grupo
cuya probabilidad de pertenencia estimada, ![]() , es máxima.
, es máxima.
Resumen
En esta lección se ha
dado una breve introducción a los modelos de regresión con variable dependiente
cualitativa, haciendo especial hincapié en los modelos de regresión logística
binaria y multinomial. Estos modelos se han presentado como una forma
alternativa de llevar a cabo un Análisis Discriminante, sin necesidad de tener
que suponer normalidad y homocedasticidad ni exigir que las variables
clasificadoras sean cuantitativas.
Los pasos a seguir para llevar a cabo un análisis de
regresión de este tipo son:
1)
Plantear el problema a
resolver determinando cuál es la variable dependiente y cuáles son las
variables independientes
2)
Estimar y seleccionar el
modelo más compatible con los datos
3)
Estudiar la bondad de ajuste
del modelo seleccionado analizando la existencia de outliers y/o observaciones
influyentes.
4)
Evaluar la bondad predictiva
del modelo utilizando métodos similares a los empleados en el Análisis
Discriminante
5)
Interpretar los resultados
obtenidos
En la lección se ha detallado cómo llevar a cabo
estos pasos para el caso particular del modelo de regresión logística binaria y
se ha ilustrado mediante el análisis de un caso práctico.
Bibliografía
Libros de Análisis
Multivariantes que contienen buenos capítulos acerca de Regresión Logística.
Desde un punto de
vista más práctico:
AFIFI, A.A. and CLARK, V.
(1996) Computer-Aided Multivariate
Analysis. Third Edition. Texts in Statistical Science. Chapman and Hall.
HAIR, J., ANDERSON, R.,
TATHAM, R. y BLACK, W. (1999). Análisis Multivariante. 5ª Edición. Prentice Hall.
KLEINBAUM, D.G. (1994) Logistic
Regression: A Self-Learning Text. Statistics in the Health Sciences. Springer-Verlag
SHARMA, S. (1998). Applied
Multivariate Techiques. John Wiley and Sons.
Desde un punto de vista más
matemático:
BISHOP, Y, FIENBERG, S. and HOLLAND, P. (1991) Discrete
Multivariate Analysis. MIT Press. Cambridge.
JOBSON, J.D. (1992) Applied Multivariate Data Analysis. Volume
II: Categorical and Multivariate Methods. Springer-Verlag.
McCULLAGH, P. and NELDER, J.A. (1989). Generalized Linear Models. Second
Edition. Chapman & Hall.
Enfocados hacia
SPSS:
FERRAN, M. (1997). SPSS para WINDOWS. Programación
y Análisis Estadístico. Mc.Graw Hill.
VISAUTA, B. (1998) Análisis
Estadístico con SPSS para WINDOWS (Vol II. Análisis Multivariante). Mc-Graw Hill.