Un gráfico sencillo pero contundente William H. Beaver, catedrático de la Universidad de Stanford, fue pionero en 1966 en investigar si los ratios financieros podían ser útiles para predecir la quiebra de las empresas. En su trabajo analizó varios ratios financieros de empresas, cinco años antes de que se produjera la quiebra, comparándolos con los ratios de empresas solventes. La siguiente figura muestra de forma gráfica el resumen del trabajo de Beaver, en el que se aprecia el poder predictivo de cada ratio.
| Beaver. W. (1966): "Financial Ratios as Predictors of Failure", Journal of Accounting Research, vol 4, suplemento 1966, pag 71-127. |
EJERCICIO: Puedes descargar esta hoja de cálculo en la que hemos preparado un gráfico igual que el de Beaver pero con datos de la quiebra de los bancos estadounidenses del 2009.
Gráficos sencillos como el de Beaver pueden ser una herramienta útil para abordar el problema de la predicción de la quiebra. Pero calcular la media no es suficiente, como reconoce elpropio Beaver en su estudio, yaque es necesario conocer alguna medida de dispersión. Comparar con la media de un sector no es útil si no se conoce al menos la desviación típica o la varianza. A pesar de ser imprescindible, no siempre se dispone de esta información. En nuestra opinión, el problema surge porque en ocasiones tenemos una idea a priori de cómo se distribuye una determinada población y no es absolutamente necesario conocer más información que la media. Pero con los ratios financieros no pasa lo mismo.
Un ejemplo nos aclara lo expuesto anteriormente: podemos leer en un periódico que la estatura media de los alemanes es de un metro y ochenta centímetros, no precisando de más información adicional sobre la desviación típica. Ello se debe a que tenemos información a priori sobre los seres humanos e imaginamos que habrá alemanes que medirán dos metros y otros más pequeños que medirán un metro y sesenta centímetros. No imaginamos alemanes de tres metros ni sospechamos de distribuciones bimodales. Por ello, conocer la media es en este caso suficiente.
Sin embargo no sucede así con la mayoría de los ratios financieros. Conocer que determinado sector tiene una rentabilidad del 20% es una información incompleta. Si la empresa que deseo analizar tiene una rentabilidad del 15% ni siquiera sabemos si es preocupante o si entra dentro de lo normal. Por ello es necesario obtener una colección de estadísticos descriptivos: media, moda, mediana, desviación típica, varianza, máximo, rango, mínimo, etc. que proporcionan una primera aproximación de los datos de partida.
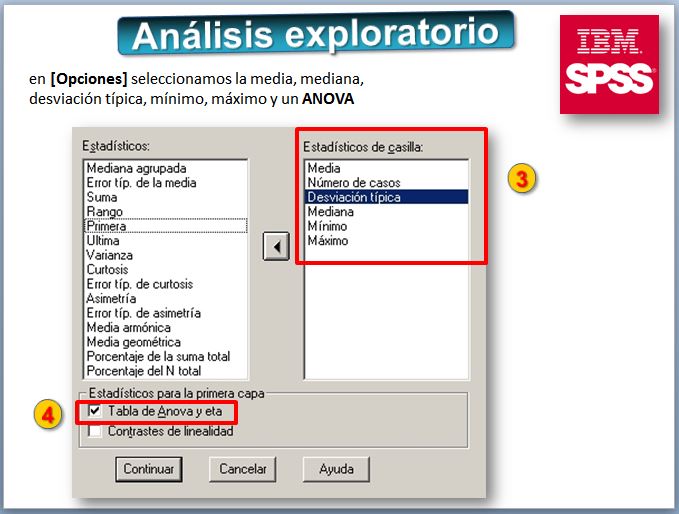
Veamos los resultados del análisis descriptivo: la comparación de medias, medianas, etc.
A simple vista, las empresas solventes presentan ratios "mejores" que los de las que quebraron. Concretamente:
- En el ratio 1, de liquidez, las quebradas presentan de media 0,3704 y las solventes más elevada, 0,4102. Pero esa diferencia de 0,0398 ¿es significativa?
- En el ratio 5, de rentabilidad, las quebradas presentan de media -0,0042 y las solventes más elevada, 0,0077. Pero esa diferencia de 0,0119 ¿es significativa?
No es tan fácil responder a la pregunta, porque hay que poner 0,0398 en relación con el ratio de liquidez. En el ratio de rentabilidad sí que podemos apreciar que la diferencia es grande, ya que los bancos solventes son varias veces más rentables que los que quebraron... pero es mejor aplicar un test estadístico, es decir, realizar un contraste de hipótesis. La hipótesis que se plantea es:
| Hipótesis nula: "las solventes y las quebradas proceden de una misma población, de tal forma que la diferencia observada entre ambas medias se debe al azar". [En lenguaje más coloquial diríamos que "apostamos porque no hay diferencias en rentabilidad -o en liquidez- entre las solventes y las quebradas"]. |
Entonces, lo que hay que decidir es si esa diferencia que hemos encontrado en la media de las quebradas y de las solventes es lo suficientemente grande como para descartar el azar. Calcularemos la probabilidad de obtener una diferencia de medias mayor que la obtenida, y si esa probabilidad es pequeña, por ejemplo menor que 0,05 (el 5%) entonces rechazaremos la hipótesis nula. Otras veces se usa el 1% o el 10%.
Podemos realizar un test de medias que permita detectar si hay diferencias significativas entre las empresas quebradas y solventes, para cada uno de los ratios. Lo vamos a hacer de tres formas diferentes:
- Un test ANOVA [lo mejor si los datos siguen una función de distribución normal, de campana de Gauss]
- Un contraste no paramétrico [recomendable si hay valores extremos y la función no es normal]
- Usando la técnica de bootstrap [hacerlo a mano es muy laborioso porque exige muchos cálculos, pero con ordenadores es muy sencillo].
¿Sacan mejores notas las chicas o los chicos? Un test de medias con bootstrap Podemos hacer un test de medias aplicando la técnica del bootstrap. Fraas y Newman explican la técnica, pero un ejemplo en hoja de cálculo nos ayudará a entenderlo con un ejemplo. Descarga la siguiente hoja:
La distribución de la diferencia de medias, si se satisfacen ciertos supuestos, es una t de Student. En este caso, un test ANOVA nos ayudará a saber si dichas diferencias pueden considerarse estadísticamente significativas. Veamos los resultados del ANOVA:
De acuerdo con este test, hay diferencias estadísticamente significativas entre los bancos quebrados y solventes en los ratios de rentabilidad. En el ratio R5, el valor obtenido (0,000) es menor que 0,05. Por tanto, se rechaza la hipótesis nula, esa diferencia es bastante grade y no parece por azar. En los de liquidez también hay diferencias pero no son estadísticamente significativas, por tanto, no se rechaza la hipótesis nula.
Como generalmente queremos encontrar diferencias, nos "alegramos"
cuando vemos los ceros...
¿Todos los cuervos son negros? El principio de falsabilidad de Popper 
Para ser rigurosos, realmente las hipótesis no se aceptan, se rechazan. Aunque veamos un millón de cuervos no podemos decir a ciencia cierta "Todos los cuervos son negros". Encambio, rechazar una hipótesis es sencillo: basta con encontrar un contraejemplo. Es decir, si encontramos un solo cuervo que no sea negro, podemos decir con rotundidad que "No todos los cuervos son negros". De hecho, existe el corvus albus. En eso se basa el principio de falsabilidad de Karl Popper.
Es decir, en nuestro ejemplo anterior:
Un problema que presentan los ratios financieros es que no siempre se cumplen esos supuestos, por lo que no es tan adecuado aplicar el test ANOVA. Por ello, para comparar las medias podemos utilizar también test no-paramétricos. Lo tenemos en:
- En el SPSS -> ANALIZAR-> PRUEBAS NO PARAMETRICAS -> DOS MUESTRAS INDEPENDIENTES
- como [Contrastar variables] seleccionamos los ratios
- como [Variable agrupación] seleccionamos OUTPUT y ponemos 0 y 1
- Seleccionamos el test, por ejemplo la U de Mann-Whitney o la Z de Kolmogorov-Smirnov
La interpretación del test es la misma... nos "alegramos" si vemos los ceros.
¿Son todos -los profesores- iguales...?Imagina que estás dudando en asistir a clase con dos profesores. Has visto las notas que han obtenido 10 estudiantes en cada uno de ellos.
¿Qué explica los accidentes de tráfico? ¿Qué variables explican que un cliente devuelva un préstamo? La base de datos de préstamos personales P2P de Lending Club contiene datos de clientes que van devolviendo el préstamo solictado y otros que no.
La variable dependiente es LOAN_STATUS_FULLY_PAID (0 fallido - 1 pagando).
Las variables independientes continuas son:
EJERCICIO: Realiza un contraste de medias ANOVA ¿Qué variables explican que un cliente devuelva el préstamo?
Tipos de variables según el nivel de medida No todas las variables son iguales y el tipo de variable nos obliga a utilizar unas técnicas u otras. El psicólogo Stanley Smith Stevens desarrolló la clasificación más utilizada en cuatro niveles o escalas de medida, de "mejor" a "peor": nominal, ordinal, intervalo y ratio.
Variables nominales (o cualitativas, categóricas o discretas). Son aquellas que no se pueden medir numéricamente. Por ejemplo el destino del préstamo (para comprar un coche, una casa o gastos médicos). También la nacionalidad o el sexo. Puedes asignar un 1 a comprar un coche, un 2 a comprar una casa y un 3 a gastos médicos pero no hay un orden, ese número no significa nada. Es decir, el 2 asignado a comprar una casa no significa que sea el doble que comprar un coche. No podemos hacer operaciones con estas variables. La moda es de lo poco que tiene sentido calcular.
Variables cuantitativas. Tienen un valor numérico (edad de una persona, el precio de un producto, el valor del ratio de endeudamiento de una empresa, ). Hay varios tipos
En la base de datos de los préstamos P2P hay variables independientes que no son continuas, sino que toman el valor 0 o 1, es decir son variables dicotómicas, también llamadas binarias o dummy.
Por ejemplo, el destino del préstamo:
- PURPOSE_CAR (préstamo para comprar un coche)
- PURPOSE_CREDIT_CARD (para cancelar una deuda contraida con tarjeta de crédito)
- PURPOSE_DEBT_CONSOLIDATION (préstamo para consolidar deudas)
- PURPOSE_EDUCATIONAL (préstamo para estudiar)
- PURPOSE_HOME_IMPROVEMENT (para reformar la vivienda)
- PURPOSE_HOUSE (préstamo para comprar una casa)
- PURPOSE_MAJOR_PURCHASE (préstamo para comprar algo grande)
- PURPOSE_MEDICAL (préstamo para gastos médicos)
- PURPOSE_MOVING (préstamo para un traslado)
- PURPOSE_OTHER (préstamo para otras causas)
- PURPOSE_SMALL_BUSINESS (préstamo para poner en marcha un pequeño negocio)
- PURPOSE_WEDDING (préstamo para casarse)
En este caso procede calcular una tabla de contingencia o de clasificación cruzada para ver si hay diferencias. Por ejemplo ¿los préstamos que se destinan a poner en marcha un pequeño negocio son más arriesgados que el resto? Podemos calcular un test de la Chi cuadrado para ver si las diferencias entre los particulares que devolvieron el préstamo y los que no son estadísticamente significativas.
- En SPSS -> ANALIZAR-> ESTADÍSTICOS DESCRIPTIVOS -> TABLAS DE CONTINGENCIA
- En Filas [LOAN_STATUS_FULLY_PAID]
- En Columnas seleccionamos las variables binarias, por ejemplo [PURPOSE_SMALL_BUSINESS] y [PURPOSE_WEDDING]
- En [CASILLAS] seleccionamos PORCENTAJES -> COLUMNA
- En [ESTADISTICOS] seleccionamos CHI CUADRADO
Veamos ahora si los préstamos que se destinan a contraer matrimonio son más arriesgados que el resto. Calcularemos también un test de la Chi cuadrado para ver si las diferencias son estadísticamente significativas.
Relación entre ser propietario de la vivienda o inquilino y devolver un préstamoLa base de datos de préstamos personales P2P de Lending Club contiene datos de clientes que van devolviendo el préstamo solictado y otros que no.
La variable dependiente es LOAN_STATUS_FULLY_PAID (0 fracaso - 1 pagando).
La variable independiente es dónde vive el prestatario:
EJERCICIO: Realiza una tabla de contingencia y un test Chi cuadrado para estudiar el efecto del régimen de tenencia de vivienda en el riesgo de devolver el préstamo. De acuerdo con estos datos ¿Qué situación es la más arriesgada? ¿y la menos arriesgada?
Ojo con darle a la manivela... Hemos visto los peligros de aplicar de forma mecánica los contrastes de hipótesis, sin pararse a pensar. Además, aunque la utilización de cualquier análisis univariante es sencilla resulta insuficiente en un tema tan complejo como la quiebra empresarial. Sabemos que son varios los factores que influyen o son responsables de la quiebra, por lo que necesariamente un análisis multivariante con capacidad para tratar varias variables simultáneamente ha de ser más apropiado.
En los siguientes apartados vamos a utilizar técnicas de análisis multivariante, que se suelen clasificar en dos tipos:
1) Supervisadas, en las que se dispone de información de variables independientes, por ejemplo, los ratios financieros o características de las empresas y la variable dependiente, como el estado "quebrado" o "solvente". Aplicaremos técnicas supervisadas como el análisis discriminante, la regresión logística, redes neuronales como el perceptrón multicapa y el análisis de supervivencia mediante regresiones de Cox. Hay muchas más técnicas, como las support vector machines o los árboles decisionales.
2) No supervisadas, en las que únicamente se dispone de los ratios financieros perono se conoce la variable dependiente, no se sabe si la empresa quebró. Lo único que podemos hacer es agrupar las empresas o los clientes y observar cómo se parecen entre sí, qué rasgos o patrones tienen en común. Usaremos técnicas como el análisis de conglomerados, el análisis de componentes principales o las escalas multidimensionales.
