Un modelo regresivo (Aznar,
1989) trata de explicar
el comportamiento de una variable exógena en función
de diversas variables explicativas (exógenas) o de valores anteriores de ella misma (endógena). En modelos más
complejos se pueden determinar conjuntamente varias variables
endógenas a través de un sistema de ecuaciones
resuelto de forma simultanea.
A lo largo de estos capítulos
se emplearán modelos más o menos complejos pero
en cualquier caso uniecuacionales, en los que sólo existirá
una variable endógena, pudiendo existir varias explicativas.
Todo este tipo de modelización parte a priori con un handicap
la existencia
de factores reales explicativos
de la variable endógena, es bien conocido que en estadística
siempre es posible incrementar el grado de explicación
por el aumento de variables exógenas en el modelo.
Conviene aclarar, que no se
ha tomado ningún partido en cuanto a la mayor o menor
validez de los modelos regresivos o de cualquier otro, antes
al contrario, se ha tratado de testear todos y cada uno de los
modelos que los autores creían podían aportar buenos
resultados. Las conclusiones son en muchos casos sorprendentes,
y avalan que en muchas ocasiones ideas apriorísticas como
por ejemplo la necesidad de modelizaciones distintas de la lineal
para la volatilidad, no son ciertas en todas las ocasiones, sino
más bien lo contrario.
En este estudio se ha pretendido
en todo momento un exhaustivo seguimiento de las posibles correlaciones
cruzadas entre variables explicativas para evitar redundancias y por supuesto de rechazar,
mediante el empleo sistemático de test estadísticos
de no significatividad, las variables que no fueran claramente
relevantes en la explicación de la volatilidad.
Para la utilizaciónde
estos modelos debemos partir de una idea ex-ante sobre la relación
entre una o varias variables y tratar de verificar que ésta
relamente exista, pero el problema no sólo reside en la
existencia de relaciones perdurables en el tiempo sino en la
forma funcional que éstas adopten, por ello en este trabajo
se emplearan diversos
modelos, que a priori
eran susceptibles de dar buenos resultados:
- Relaciones
lineales univariantes.
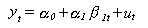
Donde:
y es la variable dependiente.
beta es la variable explicativa
Las alphas los parámetros especificados
por el modelo.
u es el término de error.
- Relaciones
lineales multivariantes.
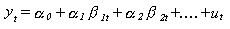
Donde:
y es la variable dependiente.
betas son las variables explicativas.
Las alphas los parámetros especificados
por el modelo.
u es el término de error.
- Modelos
de crecimiento exponencial.
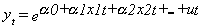
Donde:
y es la variable dependiente.
x son las variables explicativas.
Las alphas los parámetros especificados
por el modelo.
u es el término de error.
e el número e.
- Modelos
con punto de ruptura.
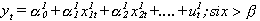
Donde:
y es la variable dependiente.
x son las variables explicativas.
Las alphas los parámetros especificados
por el modelo.
u es el término de error.
e el número e.
Siendo beta el punto de ruptura.
Otros modelos como el estudio
de eventuales relaciones logarítmicas entre precio y volatilidad,
dieron escasos o nulos resultados por los que no se reseñan
en el apartado anterior. Los ya mencionados modelos con punto
de ruptura ("piecewise
models") si se muestran muy útiles en la superación de algunos
problemas ya reseñados de la base de datos, especialmente
el inusitado incremento sufrido por la volatilidad implícita
en los peores momentos de la crisis monetaria y apuntar a un cambio
de la relación precio- volatilidad implícita en
diversos momentos del ciclo bursátil.
Este tipo de modelización permite soslayar en parte dos problemas de los modelos regresivos, por un
lado no
es necesaria la identificación de variables susceptibles
de explicar la variable
endógena al aplicarse sobre una serie de datos correlativos
de la propia variable, y además toda una serie de pautas
de actuación preestablecidas hacen más sencillo obtener la forma
funcional adecuada del modelo.
Hay que explicar que el gran problema de estos modelos, lo constituye precisamente
el cálculo
del citado punto de ruptura,
en estos capítulos sólo se especificará
uno de los puntos más relevantes de ruptura, que se produjo
en la ruptura del 3000 por parte del Ibex, comienza a existir
evidencia empírica de que puede haber un nuevo punto de
ruptura en el año 99 cuando se produce una evidente falta
de capacidad explicativa de los modelos regresivos empleados
hasta ese momento.
El paso previo al empleo de la metodología SARIMA es
la obtención
de series estacionarias,
es decir, bases de datos que cumplan los siguientes criterios
i) Media constante
en el tiempo.
ii) Varianza constante en el tiempo.
Para ello se procede a una serie de diferenciaciones y ajustes que quedan explicados paso
a paso en el momento en que se utilicen a lo largo del trabajo.
A la hora de especificar un modelo
ARIMA son necesarios
3 parámetros:
i) El retardo de la parte autorregresiva
(AR) que viene explicitado
por el subíndice p en la siguiente fórmula:
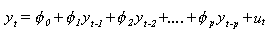
Donde:
y es la variable dependiente
Las phi representan en este caso, a los parámetros
especificados por el modelo.
u es el término de error.
En realidad la relación
matemática no hace sino poner en evidencia que la observación
de la variable y en el período t depende de las misma
variable y en t-1, t-2,... y t-p.
ii) El retardo de la parte de medias móviles
(MA), q en la fórmula
siguiente:
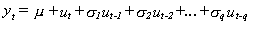
Donde:
y es la variable dependiente
Las sigma representan en este caso, a los parámetros
especificados por el modelo.
u son los términos de error.
La significación de
este tipo de modelos es también bastante clara, se trata
en suma de explicar la variable y en t en función de una
constante y de una corrección de q errores del modelo
en los períodos anteriores.
iii) Número de veces que hemos de diferenciar (I)
la serie para hacerla
estacionaria.
Se entenderá por diferencial de yt, la diferencia entre la volatildad
en t y t-1, es decir:
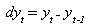
Donde:
d indica que se trata de la diferencial
de la variable de que se trate
y es la variable dependiente
En ocasiones se emplea la diferenciación logarítmica para
obtener un mayor alisado de la serie, sin embargo, este tipo de diferenciación
no dió excesivos buenos resultados a la hora de modelizar
las series de datos empleadas en este estudio.
La utilización de estos
modelos permite constatar un hecho
que no deja de ser preocupante, la volatilidad en t no es independiente
de la manifestada en otros períodos inmediatamente anteriores,
poniendo en tela de
juicio las propias fórmulas valorativas de opciones ,
empleadas por la práctica totalidad de los participantes
en el mercado.
Antes de entrar en el siguiente
apartado, sería conveniente explicar las principales diferencias
entre los modelos ARIMA y los de la familia ARCH, mientras que los ARIMA se aplican sobre series homocedásticas, es decir, de varianza constante,
los
ARCH se caracterizan por tratar de modelizar precisamente la
heterocedasticidad de la serie.
Por lo tanto mientras que en los modelos ARIMA se debe de alisar
la serie como paso previo a la modelización de la misma,
ésto no es necesario en los ARCH, lo que no es por si
mismo una ventaja al obligar a elegir una de las múltiples
posibilidades de modelización ofrecidos por los ARCH que
se tratarán en el apartado posterior.
Los resultados del trabajo
de Poon
y Taylor (1991) hacen
intuir que los modelos ARIMA y cualquiera de los ARCH no son
en principio excluyentes, mientras los ARIMA son válidos para identificar
los cambios de tendencia en volatilidad, en el caso de los heterocedásticos se
observa una mayor inestabilidad en el resultado, aunque la serie
prevista se ajuste más a los frecuentes cambios en la
volatilidad real. En resumen, la serie, en este caso generada
por un GARCH (1,1), prevista por el modelo heterocedástico
se ajustaba mejor, pero era más volátil en la cuantía
de los errores.
Un tema que no se trata en este
trabajo es el análisis de la posible existencia de estacionalidad (la S de los modelos SARIMA) en la
series de volatilidad, se ha de reconocer que existen períodos
concretos en los que se producen cambios de una manera casi sistemática
en la volatilidad implícita. Se puede citar el fenómeno
de reducción de la volatilidad los días inmediatamente
anteriores a puentes festivos (en los días inmediatamente
anteriores a la festividad de semana santa de 1996, la volatilidad
implícita se redujo desde el 17% a niveles cercanos al
13% en las series "at-the-money") pero sería
muy difícil llegar más lejos en el análisis
por la relativa limitación de la base de datos.
Hay sin embargo una excepción a esta afirmación anterior,
se podrá constatar a lo largo de la presentación
de los resultados de los modelos que recurrentemente aparece
un efecto estacional (que será denominado pseudoestacional
en este trabajo) que coincide con el período de cálculo
de la volatilidad histórica homocedástica que se
esté modelizando.
A modo de introducción
sería conveniente recordar que estos modelos son relativamente
novedosos, su desarrollo comienza con los trabajos de Engle (1982, op. citada) y se muestran especialmente
útiles según Crouhy y Rockinger (op.
citada) para:
- La modelización de una volatilidad
no constante en el
tiempo.
- Recoger
en modelos teóricos la evidencia empírica de que la volatilidad
se manifiesta en olas.
- Identificar la existencia de una memoria
importante en el proceso.
- Predicción de la volatilidad futura
A) ARCH
El modelo ARCH fue desarrollado
por Egle en 1982 y se basa en la explicación de la volatilidad
condicional como una función lineal de q errores pasados de predicción elevados al cuadrado
(los epsilon de la fórmula).
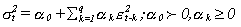
Donde:
sigma es la variable condicional
Los alpha son los parámetros especificados
por el modelo
Epsilón son los términos de error
Tanto este modelo como el resto
de los que se tratará a continuación, que no son
sino desarrollos más o menos complejos del mismo, definen
la volatilidad
condicional,que es
la única que se puede predecir por las hipótesis
del modelo, como la volatilidad condicionada a la información
existente en ese periodo
(denotada por Phi en la formula siguiente).
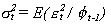
Donde:
Epsilón en t es el "shock" o error
de predicción
Phi representa la información existente
en t y que no existía en t-1.
Los modelos tradicionales trataban sólo la volatilidad
incondicional, es decir:
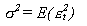
Si se piensa en el caso de
la volatilidad
implícita, ésta
viene condicionada por toda la información existente hasta
el período considerado, por lo que el concepto de "shock"
de volatilidad podría ajustársele sin excesivos
problemas. Es tal vez por esta razón por la que es posible
llegar a una conexión de las volatilidades implícita
y condicional sin excesivos problemas, a pesar de que no exista
relación funcional alguna entre ellas
En cuanto a la memoria del proceso, se corresponde con la suma de todos los coeficientes
alfa, en concreto:
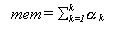
Siendo r
el número de coeficientes alpha distintos de 0.
De acuerdo con un modelo ARCH(1) se puede prever la volatilidad s períodos
más adelante como sigue:
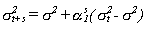
Siendo sigma cuadrado la volatilidad incondicional, es decir, aquella
que no depende del período en que nos encontremos. En
el largo plazo es destacable que la volatilidad condicional e
incondicional tienden a aproximarse en cualquier caso, como veremos
más tarde es muy raro que alpha1 sea mayor que la unidad,
ésto no es así necesariamente en los modelos GARCH.
B) GARCH
Este modelo fue desarrollado
por Bollerslev (1987), extendiendo el modelo ARCH
para incluir retardos en la varianza condicional. En definittiva
un GARCH
es un modelo ARCH infinito,
un GARCH (p,q) se define como:
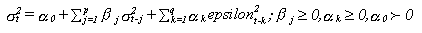
Donde:
sigma es la variable condicional
Los alpha
y beta son los parámetros
especificados por el modelo
Epsilón son los términos de error
Si p es cero el proceso se
reduce a un ARCH(q). Si tuviésemos por ejemplo un GARCH
de reducida p, que son los más comunes en los estudios
de mercado, sus propiedades vendrían a ser equivalentes
a un ARCH con una q elevada, en general con q mayor o igual a
20.
Como quiera que por las hipótesis
propias al modelo:
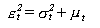
Se puede reformular un GARCH(p,q) como sigue:
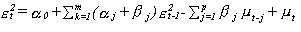
Donde m es el máximo entre p y q, y mu no manifiesta correlación
con las otras series.
La previsión en un modelo GARCH(1,1) se efectúa como
sigue:
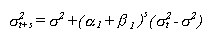
Sólo en el caso de que
alpha1 más beta1 sea inferior a 1 la volatilidad prevista
decrecerá hacia la incondicional, en ese caso se dice
que el modelo es integrado.
C) EGARCH o "exponential GARCH"
Este modelo surge para paliar un problema de los modelos GARCH consistente en
que los
efectos de una "sorpresa", entendida como información inesperada
por el mercado, son los mismos se trate de una noticia negativa
o positiva. Sin embargo parece empíricamente demostrado
que los picos en volatilidad coinciden con caidas de mercado,
por lo que una mayor asimetría de la distribución
de volatilidad sería conveniente. Este modelo a pesar
de su complejidad teórica permite estudiar desde otro punto de
vista la asimetría precio-volatilidad que ya se estudia en la parte regresiva,
pues no es necesario acudir a la serie de precios para la modelización.
En un modelo EGARCH(1,1) la varianza
condicional se escribiría
como sigue:
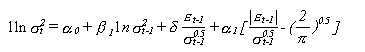
Donde:
sigma es la variable condicional
Los alpha son los parámetros especificados
por el modelo
Epsilón son los términos de error
Delta el parámetro de asimetría
Pi es el número pi
Un coeficiente delta estimado negativo confirmaría
la presencia de un sobreimpacto de las noticias negativas, la
contribución de un "shock" positivo en la volitilidad condicionada es:
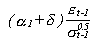
Por el contrario un "shock" negativo:
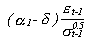
La asimetría de la volatilidad condicionada la mediría
el siguiente ratio:
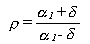
D) Non-Linear Assymmetric ARCH (AGARCH)
Desarrollado por Engle(1990) y Sentana
(1991). Un AGARCH
(1,1) :
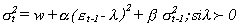
Donde:
sigma es la variable condicional
w es la variable incondicional
alpha
y beta son los parámetros
especificados por el modelo
Epsilón son los términos de error
Lambda el coeficiente de asimetría
Se formulan a continuación
algunos
modelos susceptibles de ser probados en nuestro mercado, que no han sido probados en el presente
trabajo.
E) Otros modelos Heterocedásticos
La lista de modelos heterocedásticos
es muy amplia, de hecho una gran parte de la innovación
de la ciencia econométrica se ha centrado en los últimos
años en el desarrollo de modelos que se ajusten cada vez
más a las series de volatilidades.
- Glosten, Jagannathan y Runkle
desarrollan el GJR-ARCH en 1989. Un GJR-ARCH(1,1) se expresaría
como sigue:
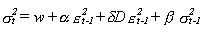
Donde:
sigma es la variable condicional
Los alpha,
beta, delta son los
parámetros especificados por el modelo
D es una variable binaria que toma el
valor 0 o 1.
Epsilón son los términos de error
D es una variable que toma
el valor 1 en t, si el error en t-1 es negativo y 0 si el error
en t-1 es positivo.
- TGARCH
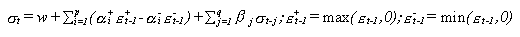
Donde:
sigma es la variable condicional
Los alpha
y beta son los parámetros
especificados por el modelo
Epsilón son los términos de error que
se definen como doble variable tal y como se expresa en la fórmula
Este breve repaso de los modelos
heterocedásticos debe servir para realizar una reflexión
previa, estos modelos fueron diseñados para modelizar la
volatilidad condicional del rendimiento de un activo financiero, puesto que en este trabajo las volatilidades
que se estudian son la volatilidad histórica homocedástica
y sobre todo la implícita cabría preguntarse si
esta última es susceptible de ser aproximada por la volatilidad
condicional modelizada mediante cualquiera de las formulaciones
anteriores.
En principio la volatilidad implícita
no corresponde a una volatilidad real o condicionada del rendimiento de ningún
activo financiero, para aplicar un modelo heterocedástico
habría que realizar una serie de hipótesis:
i) Que la volatilidad implícita en
t es una volatilidad condicionada
a toda la información conocida en t-1.
ii) Que existe una volatilidad implícita
incondicional hacia
la que tendería el modelo, que correspondería con
la volatilidad del rendimiento a un período concreto.
iii) Y por último que disponemos de una base
de datos lo suficientemente amplia.
La primera hipótesis no es en principio
ilógica, de
hecho la volatilidad implícita se ajusta muy bien a la
información existente en el mercado en cada momento. Se
puede afirmar que cualquier noticia o cambio brusco en precio
va a alterar la volatilidad implícita negociada, en términos
de Engle (op. citada) va a producir un "shock" en la
volatilidad negociada.
La segunda hipótesis es ya mucho
más difícil de manejar, se podría tal vez afirmar que en el
futuro la volatilidad implícita tenderá a aproximarse
a la histórica, no queda claro a qué período,
más un "gap" que resulte justificable entre
ambas en el largo plazo. Sin embargo este punto queda muy lejos
de ser evidente y deberá ser objeto de posteriores trabajos.
El tercer punto incide en algo ya conocido, todos los trabajos
citados hasta este momento disponían de muchas más
observaciones, ésto es especialmente importante para los
modelos ARCH, pues estudian la persistencia de la volatilidad
en el largo plazo y la existencia de ondas de volatilidad. Todos
los resultados de este trabajo quedarían puestos en evidencia
si la volatilidad se encontrara en la misma onda desde que comenzaron
a negociarse opciones sobre el IBEX.
Si se verificaran
estas hipótesis
en realidad se estaría aceptando que la volatilidad implícita
se aproxima a ser la volatilidad histórica (homo o heterocedástica)
del rendimiento a un período concreto más un gap
sostenible, es decir, volatilidad implícita= gap + volatilidad
histórica a n días.
El tratamiento que se ha hecho
para aplicar la modelización heterocedástica a
la volatilidad implícita, no va a ser la definición
de la función de rendimientos de la volatilidad implícita
debido a los evidentes problemas de cálculo que ello conllevaría,
sino que se va a proceder a modelizar los rendimientos del IBEX
mediante esta metodología, tratando de obtener relaciones
válidas entre las volatilidades condicionales empleadas
y la volatilidad implícita.