Tema 1. Las Finanzas
Leemos en El Periódico que la fortuna de Jordi Pujol  , ex-presidente de La Generalidad de Cataluña creció desde los 840.000 euros en 1980 hasta los ocho millones en 1992. Como economistas podemos preguntarnos si esa rentabilidad es normal o es poco creíble. La Cuenta Nómina de Bankinter ofrece unos atractivos intereses ¿qué opinión te merece? Plataformas electrónicas como Circulantis.com ofrecen a inversores particulares la posibilidad de adquirir pagarés de empresas ¿Es una buena opción?
, ex-presidente de La Generalidad de Cataluña creció desde los 840.000 euros en 1980 hasta los ocho millones en 1992. Como economistas podemos preguntarnos si esa rentabilidad es normal o es poco creíble. La Cuenta Nómina de Bankinter ofrece unos atractivos intereses ¿qué opinión te merece? Plataformas electrónicas como Circulantis.com ofrecen a inversores particulares la posibilidad de adquirir pagarés de empresas ¿Es una buena opción?

Ninguna de esas preguntas tiene una respuesta sencilla, porque para valorar cualquier operación financiera, como pedir un préstamo, invertir en bolsa, depositar un plazo fijo en el banco, contratar un depósito o prestar a empresas vía crowdlending hay que hacer números. Hay fórmulas muy complicadas pero las Matemáticas Financieras que empleamos en la asignatura son bastante más sencillas. Son la herramienta de los financieros. Hoy en día todos los cálculos se realizan con ordenador, por lo que resolveremos todos los ejercicios de la asignatura con la hoja de cálculo. En esta lección aprenderemos primero algunos conceptos introductorios sobre las Finanzas y en particular de qué se ocupa "el de finanzas" en la empresa. El segundo apartado trata sobre una de las actividades más importantes de las Finanzas, que es la valoración financiera, presentando las leyes financieras. Finalizamos con conceptos de Matemáticas Financieras, es decir, las matemáticas que nos permiten manejar tipos de interés y realizar las operaciones de capitalización y descuento. Pero, además, las Finanzas no solo son fríos números, y muchas decisiones financieras se pueden explicar mejor desde una perspectiva psicológica. Son las llamadas Finanzas conductuales  . Por ese motivo, en la figura hemos añadido a Homer Simpson y Mr Spock, de los que hablaremos al finalizar la lección.
. Por ese motivo, en la figura hemos añadido a Homer Simpson y Mr Spock, de los que hablaremos al finalizar la lección.
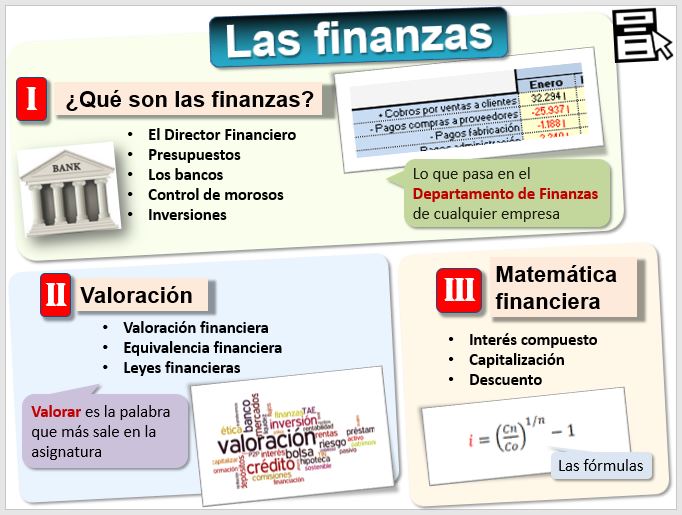
 Puedes descargar una hoja de cálculo con los ejemplos que veremos en teoría -> [01-Teoria.xls].
Puedes descargar una hoja de cálculo con los ejemplos que veremos en teoría -> [01-Teoria.xls].
1.1) ¿De qué se ocupa "el de finanzas" en la empresa?
¿Qué tienen en común actividades tan diversas como tomarse una cerveza, comprar un tractor o construir una carretera?

Las tres actividades tienen en común que al final hay que pagar. La palabra "Finanzas" viene del latín "fīnis" y su etimología significa eso, lo que viene al final de cualquier transacción, que es pagar. Podemos definir las Finanzas como "una rama de la Economía, cuyo campo de estudio es el proceso de obtener unos fondos -dinero- para realizar unas inversiones". La definición destaca las dos grandes áreas de estudio en que dividimos las Finanzas (Financiación e Inversión). Con el ejemplo de la cerveza, el tractor y la carretera enfatizamos que las Finanzas afectan a individuos, empresas y administraciones. Ya tenemos una primera idea de a lo que se va a dedicar "el de Finanzas".
Cualquier empresa se organiza en distintos departamentos. En la siguiente figura vemos la estructura típica de una empresa cualquiera.

Una estructura típica incluye una dirección general, unas direcciones de departamentos (Finanzas, Marketing, Producción, Recursos Humanos, entre otros) y otras funciones como secretaría, almacén, etc. A modo de ejemplo, veamos el de Telefónica e IKEA.

Como vemos en la figura, el de Finanzas es un departamento importante para Telefónica e Ikea. Normalmente el Director de Finanzas depende directamente del Presidente Ejecutivo. Nadie duda de la importancia del CFO (Chief Financial Officer), el nombre que recibe en inglés, muchas veces es la mano derecha del Director Ejecutivo (CEO o Chief Executive Officer). Muchos de los Directores Ejecutivos suelen ser antiguos Directores de Finanzas. La siguiente figura muestra los responsables del Departamento de Finanzas y algunas de las actividades que realizan:
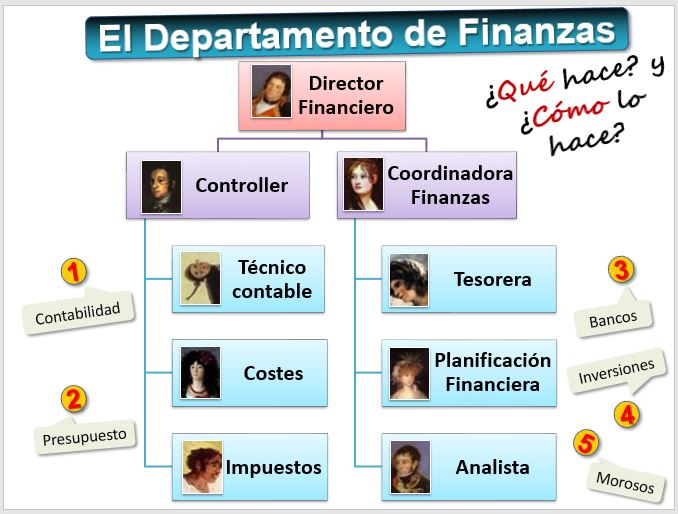
Como vemos, "los de finanzas" se ocupan de todo lo relacionado con el dinero. Existen muchos variantes, en este caso la empresa de la figura ha optado por dos cargos que dependen del Director Financiero: el Director de Gestión o controller y la responsable o coordinadora de finanzas. Naturalmente, no es la única posibilidad. Por ejemplo, es muy común que el controller dependa directamente de la Dirección General y supervise a todos.
El controller y su equipo:
- Llevan la contabilidad de la empresa: su registro, custodia y papeleo.
- Generalmente, se suelen ocupar de coordinar todas las actividades administrativas, de hecho, en muchas empresas se le llama también Jefe de Administración, incluyendo los impuestos. Si la empresa es muy pequeña también se encarga de los temas informáticos.
- Prepara los informes contables y financieros.
- Elabora los presupuestos.
- Se ocupa del control de la gestión, tanto financiera como comercial.
- Se ocupa del cálculo de los costes, necesario para saber con precisión lo que cuesta producir un producto.
La coordinadora de finanzas y su equipo:
- Se ocupan de la tesorería.
- De obtener financiación y de las relaciones con los bancos.
- De realizar los pagos, tanto de los pedidos y compras como a los empleados a través de la nómina o a Hacienda al pagar los impuestos.
- Llevan las relaciones con los inversores y accionistas.
- Aprueban las inversiones y gastos de la empresa. Suele ser la mano derecha del Director Ejecutivo.
- Todo lo relacionado con los seguros.
1.2) Los presupuestos
Una actividad que realiza el departamento es la planificación financiera. Realizan los presupuestos. Aunque estemos en febrero, saben que en julio habrá que pagar las horas extras de los empleados y tener el dinero disponible. Porque también se ocupan de la tesorería de la empresa. En el presupuesto se trata de recoger todos los cobros y pagos previstos, algunos serán muy exactos, como los pagos al banco por intereses de un préstamo, pero en otros casos hay que realizar hipótesis y previsiones, por ejemplo, sobre la evolución de las ventas.
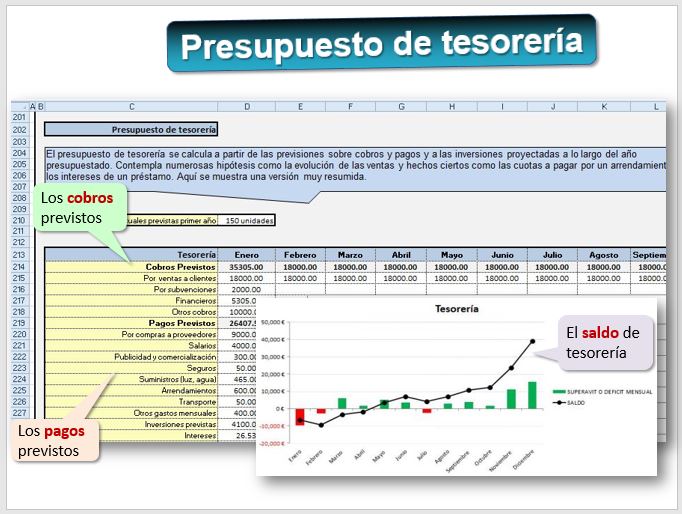
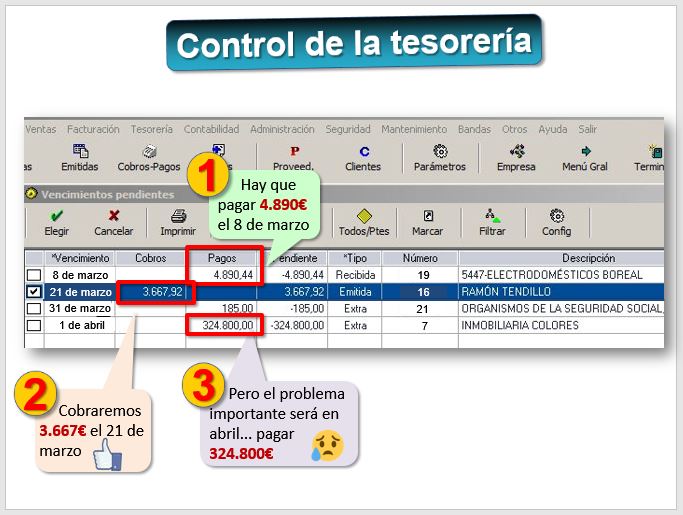
Cualquier programa de contabilidad permite llevar un control de la tesorería. En el siguiente vemos los cobros y pagos previstos. En la pantalla podemos apreciar que la empresa va a tener un pequeño problema en marzo que quizá podría solucionar retrasando ese pago a Electrodomésticos Boreal, o negociando con un cliente, Ramón Tendillo, a ver si puede pagar antes (ofreciendo un descuento) ... pero nada que ver con el problema que viene después, por el pago a la Inmobiliaria Colores.
1.3) Las relaciones con los bancos y administraciones
El Departamento es responsable de las relaciones con los bancos: desde pedir préstamos a colocar el dinero excedente en productos financieros. Y, si la empresa es pequeña, también a veces se encarga de relacionarse con las administraciones públicas en los temas de dinero, como las liquidaciones de impuestos, o presentar documentos mercantiles. Porque muchas veces el departamento es "Administración y Finanzas".

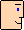 Comparar productos financieros
Comparar productos financieros
El Director de Finanzas debe conocer bien la oferta financiera actual. Muchas páginas web comparan los productos y servicios financieros.
EJERCICIO: En comunidades financieras independientes como Rankia.com, los expertos y colaboradores analizan y comparan productos financieros, proporcionando listados sobre las mejores cuentas bancarias (http://www.rankia.com/comparador/cuentas) o tarjetas de crédito (http://www.rankia.com/comparador/tarjetas), entre otros.
1.4) Los morosos
Una tarea muy importante es el control de los morosos, clientes que están retrasándose en el pago. Es fundamental llevar un buen control, para evitar que los vendedores sigan sirviendo pedidos a esos clientes, a pesar de que no pagan, como muestra la siguiente figura.
1.5) Las inversiones y los gastos

Son típicas las reuniones entre:
- 1) El gerente de la empresa
- 2) El responsable de finanzas, sentado a su lado
- 3) La responsable de producción, que quiere comprar una máquina nueva
- 4) El director de marketing, que plantea una ambiciosa campaña para vender por Internet
- 5) El responsable de personal, que propone contratar a dos empleados nuevos...
El responsable de finanzas realiza una valoración estudiando aspectos como la rentabilidad, el riesgo y la liquidez de las ideas y proyectos presentados.

2) Valorar
La palabra valorar es la que más se repite en la asignatura. El diccionario define valorar como "señalar el precio de algo" [RAE], pero no es una definición suficientemente clarificadora; quizá algunos poetas y literatos nos puedan ayudar.

- "Todo necio confunde valor y precio" (Antonio Machado
 ). Nos dice que no son sinónimos. Muchos padres no tienen un trabajo remunerado, sino que atienden el hogar, cuidan a los hijos y cobran 0€ por hacer su trabajo. Pero ¿cuánto vale un zumo de naranja cuando estamos malitos?
). Nos dice que no son sinónimos. Muchos padres no tienen un trabajo remunerado, sino que atienden el hogar, cuidan a los hijos y cobran 0€ por hacer su trabajo. Pero ¿cuánto vale un zumo de naranja cuando estamos malitos?
- "Hoy en día el hombre conoce el precio de todo y el valor de nada" (Oscar Wilde
 ). Conocer el precio es sencillo, pero el valor es complicado.
). Conocer el precio es sencillo, pero el valor es complicado.
- "Si quieres conocer el valor del dinero, trata de pedir prestado". (Benjamin Franklin
 ). El tipo de interés es el precio del dinero.
). El tipo de interés es el precio del dinero.
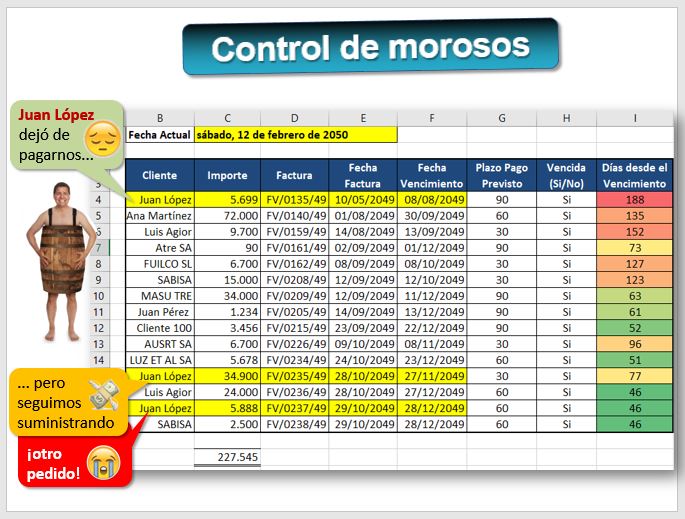
El precio lo fija la oferta y la demanda y es objetivo. El valor es subjetivo, depende de cada uno, y tiene que ver con la utilidad percibida, las expectativas futuras de beneficios y el riesgo. Veamos algunos ejemplos de situaciones en las que hay que realizar una valoración:
- Antes de comprar unas acciones en bolsa, previamente, las valoramos y si pensamos que están baratas las compramos [¿Se valoró bien AENA a 58 euros cuando salió a bolsa? AENA hoy] [ojo, split].
- Un inversor que quiera comprar una empresa tendrá que valorarla. Pero en la empresa hay conceptos muy diversos: terrenos, máquinas, inversiones financieras, clientes, deudas...
- Un camarero quiere tener su propio bar, por el que le piden un traspaso, debido a la clientela existente y a la maquinaria.
- Un constructor que compra un terreno urbano para edificar pisos tiene que valorarlo en función de los pisos que se podrán hacer allí.
- ¿Cómo valorar una patente o una marca?
- Un filántropo desea donar parte de su fortuna a proyectos que tengan un impacto social. ¿Qué proyecto es más interesante?, ¿uno que crea varios puestos de trabajo u otro que logra reducir la contaminación ambiental?
2.1) Valoración financiera
En muchas situaciones, cuando alguien pone un ejemplo poco acertado, se le dice despectivamente "estás comparando peras con manzanas". Una ventaja en Finanzas es que gracias a que usamos el dinero, sí podemos comparar peras con manzanas. Como vemos en la figura, financieramente, 1 kilo de peras equivale a 2 kilos de manzanas.

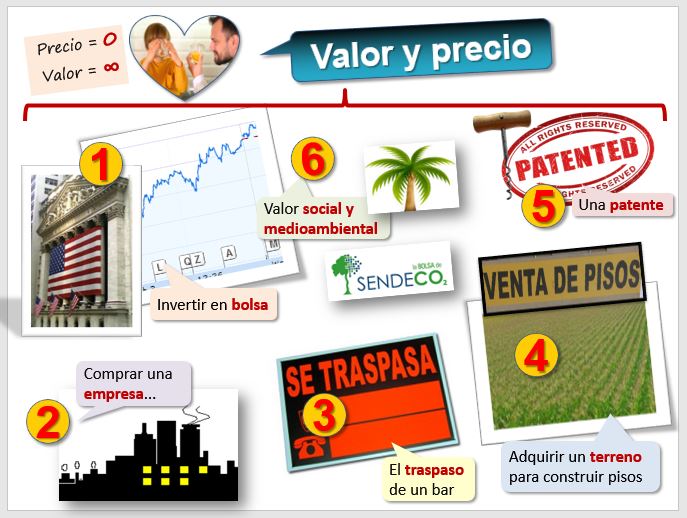
Las técnicas de valoración que vamos a aprender se pueden aplicar a múltiples situaciones. La figura muestra el balance de una persona que lleva 20 euros en el bolsillo y un móvil que costó 100€ y del que debe 70€. Las partidas analizadas están en:
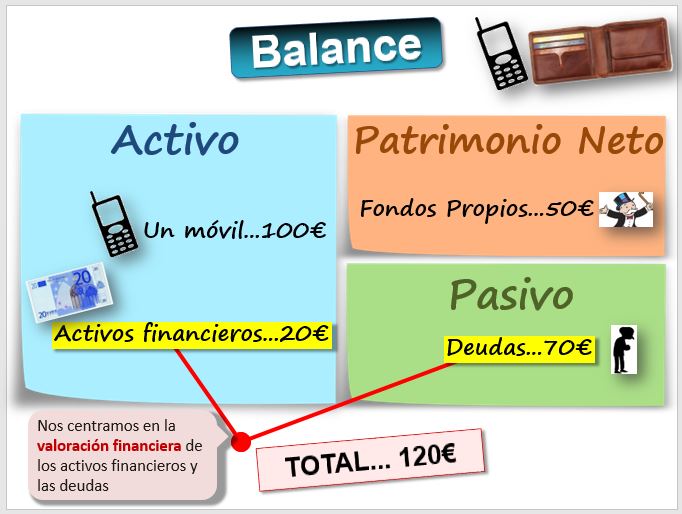
Para realizar la valoración de los activos existen varios métodos y criterios, uno puede ser el coste de adquisición del móvil -el criterio que usa el contable-, otro, el precio de mercado actual -nuevo o de segunda mano- o también podemos valorarlo por su capacidad futura para generar resultados -por ejemplo, puedo abrir un negocio de alquiler de móviles-. De forma específica, la valoración financiera trata del conjunto de metodologías que tratan de obtener el valor de un conjunto de activos financieros (unas acciones o bonos que tenemos) o de pasivos financieros (una deuda que ha contraído la empresa por un préstamo que ha solicitado). En el ejemplo el "activo financiero" se trata de dinero en metálico, si bien en una empresa podrían ser unas acciones de otra empresa que hay que valorar. En cuanto a
las "deudas" podría ser un préstamo que tiene que devolver en diversas cuotas de las que hay que calcular el tipo de interés efectivo.
Veamos ahora el balance de una empresa. Lo veremos en detalle en la lección 3, pero en el Activo, en el Patrimonio Neto y en el Pasivo ya intuimos partidas que habrá que valorar, como patentes, terrenos, inversiones financieras...

2.2) Principio de equivalencia financiera
¿Qué prefieres? ¿Recibir 1.000€ ahora o dentro de un año? Mejor ahora, naturalmente. Si nos dan a elegir entre una cantidad de dinero ahora u otra dentro de un año, tendrán que ofrecerme más dinero. Por tres motivos:
- El riesgo. En un año pueden pasar muchas cosas.
- La inflación. Reduce el poder de compra del dinero, todo será más caro dentro de un año.
- Prefiero consumir ahora que dentro de un año. Si el jefe me ofrece quedarme sin vacaciones este año y compensarme dentro de un año, le voy a pedir a cambio más días.
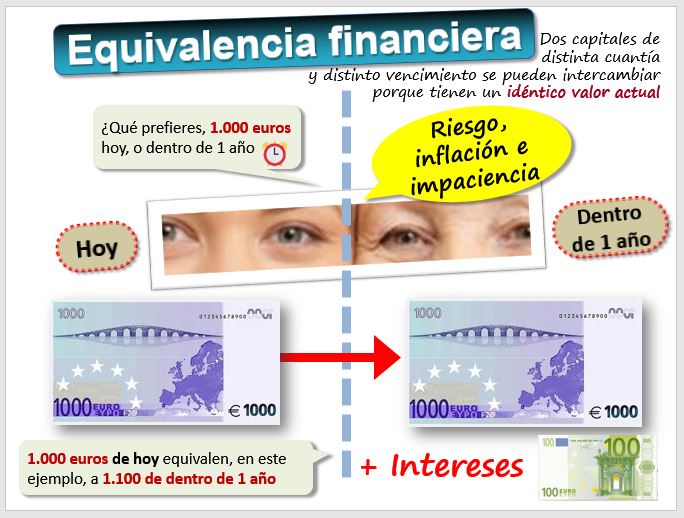
En el ejemplo, vemos que para esa persona 1.000€ euros ahora equivalen a 1.000€ más una cantidad, que son lo que llamamos los intereses. El tipo de interés es el precio del dinero.
Vamos a suponer que los intereses son 100€. Diremos que 1.000€ ahora equivalen a 1.100€ dentro de un año. En ello consiste el "principio de equivalencia financiera": reemplazamos un capital inicial C0 en un momento dado t0, (C0, t0) por otro capital final Cn en otro momento tn, (Cn, tn) de forma que nos da igual elegir uno u otro. En otras palabras, el principio de equivalencia financiera supone que dos capitales de distinta cuantía y distinto vencimiento se pueden intercambiar porque tienen un idéntico valor actual. Para determinar la equivalencia financiera entre ambos capitales se aplica una fórmula matemática -llamada ley financiera- con la que se calculan los intereses.
2.3) Leyes financieras: capitalización y descuento
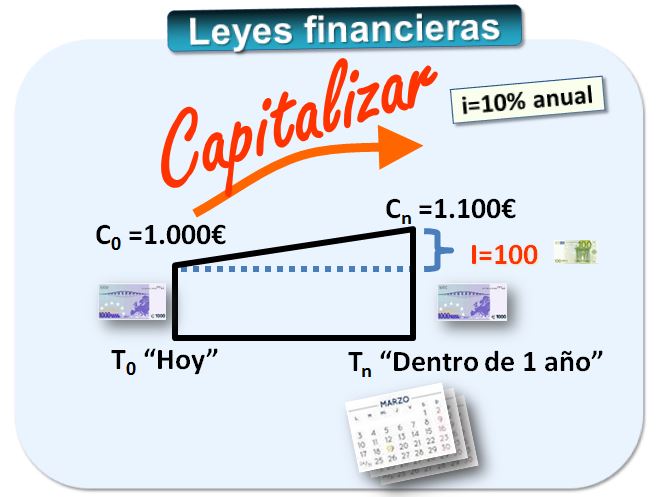
A) Una persona realiza un depósito en el banco de 1.000€. Dentro de un año recibe 1.100€. Eso es capitalizar, es decir, sumar a un capital actual los intereses devengados.
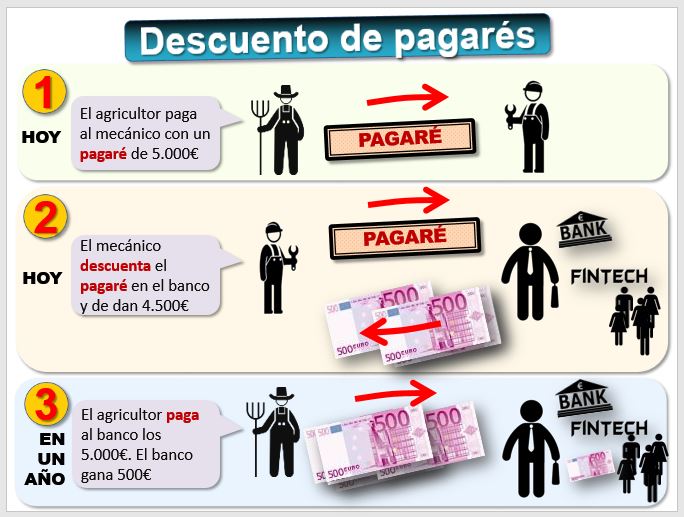
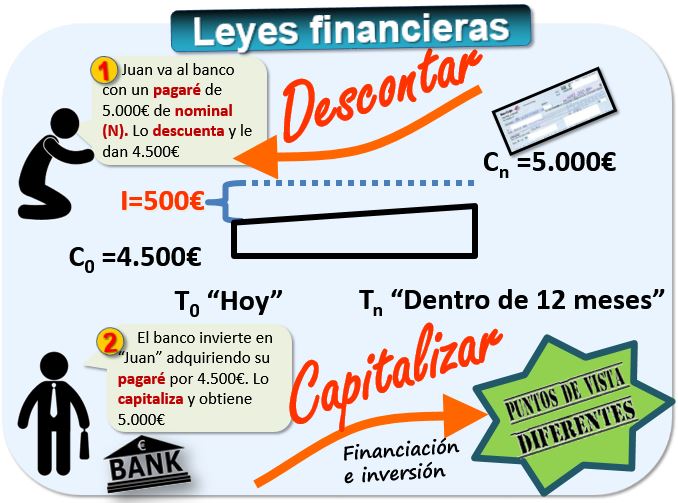
B) Una empresa de reparación de maquinaria tiene como cliente a un empresario del sector agrario al que ha reparado una máquina por 5.000€ y que paga mediante un "pagaré", que es un documento parecido a este:

El mecánico puede ir al banco con ese documento y le entregarán ya una cantidad de dinero, por ejemplo, 4.500€. El banco ha descontado 500€ en concepto de intereses. Cuando llegue la fecha de vencimiento, la empresa del sector agrícola pagará al banco los 5.000€. El banco gana 500€ con la operación.
Eso es descontar o actualizar, es decir, restar de un capital futuro los intereses que éste todavía no ha devengado. El valor actual de esos 5.000€ son 4.500€.
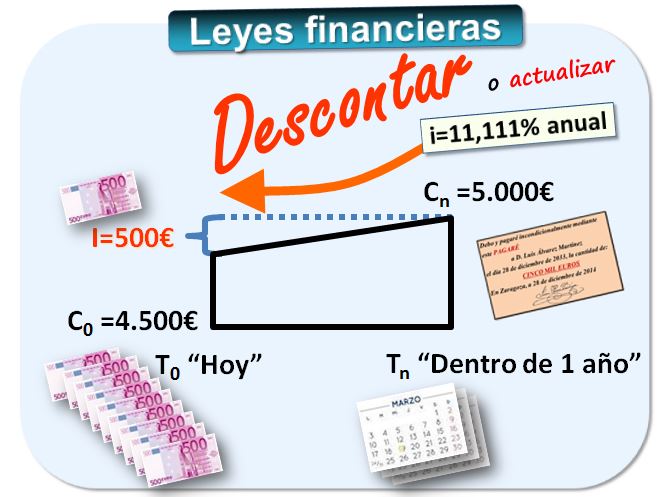
Si la empresa de reparación invierte esos 4.500€ -es decir, capitaliza- y logra un 11,1111% anual obtendrá 5.000€ dentro de un año. Diremos que son operaciones equivalentes. En este caso, lo que para la empresa es una operación de financiación (descontar un pagaré en el banco para conseguir dinero), para el banco es una operación de inversión (invierte un capital y obtiene un rendimiento unos meses más tarde). Como vemos, descontar y capitalizar son las dos caras de la misma moneda.
 Maximizar el valor actual de las decisiones
Maximizar el valor actual de las decisiones
En 1970 se otorgó el Premio Nobel de Economía a Paul Samuelson  , autor en 1937 de la “Teoría de la Utilidad Descontada”, que afirma que los consumidores tratan de maximizar el valor actual de sus decisiones. Por ejemplo, una persona se quiere jubilar con 500.000€ ahorrados. Puede calcular cuánto debe ahorrar cada mes aplicando simplemente la fórmula del descuento exponencial anteriormente vista.
, autor en 1937 de la “Teoría de la Utilidad Descontada”, que afirma que los consumidores tratan de maximizar el valor actual de sus decisiones. Por ejemplo, una persona se quiere jubilar con 500.000€ ahorrados. Puede calcular cuánto debe ahorrar cada mes aplicando simplemente la fórmula del descuento exponencial anteriormente vista.

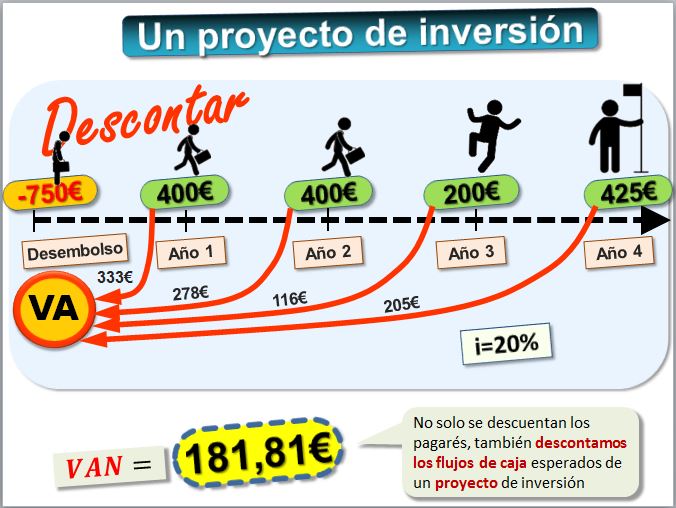
No solo se descuentan los pagarés, también se descuentan los flujos de caja estimados en un proyecto de inversión. La siguiente imagen muestra un proyecto de inversión en el que nos piden 750€ y se espera obtener un dinero a lo largo de varios años. Lo veremos en detalle en el tema 6.
3) Interés simple e interés compuesto
En el interés simple, los intereses que se reciben no generan nuevos intereses. Por ejemplo, un depósito o plazo fijo en el banco puede proporcionar unos intereses elevados, pero esos intereses van a una cuenta corriente o libreta y allí el tipo de interés es cero. En cambio, en el interés compuesto los intereses que se reciben sí que generan nuevos intereses. Sobre todo, se utiliza en operaciones cuya duración es superior a un año. Por ejemplo, si se pide un préstamo y no se devuelve, los intereses que devenga se acumulan y generan nuevos intereses que con el paso del tiempo pueden ser muy elevados [ejemplo créditos rápidos]. Se suele atibuir a Einstein la frase "compound interest is the most powerful force in the Universe". Otros científicos la han utilizado para indicar que unos tipos de interés muy altos son un arma que destruye a las personas sin romper los edificios. La frase es una manera indirecta de reconocer el poder de la Economía y sus efectos, que pueden ser tan devastadores como una bomba atómica [ejemplo deuda Grecia].

3.1) Capitalización con interés simple
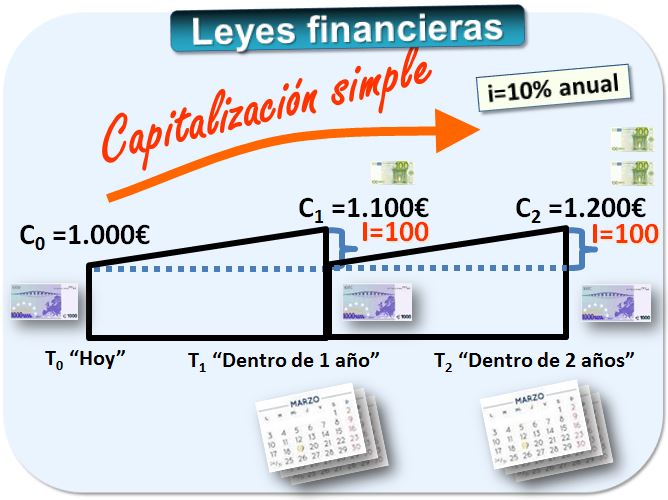
La capitalización simple suele aplicarse cuando el periodo de capitalización es inferior a un año, aunque puede aplicarse en periodos superiores. Veamos el siguiente ejemplo. Antes hemos visto que capitalizar un capital inicial de 1.000€, a un tipo de interés del 10% anual durante 1 año genera 100€ de intereses.

El capital final (también llamado montante) es 1.100€. Que es igual al capital inicial (1.000€) más los intereses. Los intereses se calculan multiplicando el tipo de interés (10%) por el capital inicial. Como solo tenemos un año, multiplicaremos por un periodo.
Veamos ahora un ejemplo con dos años. Un plazo fijo de 1.000€ en el banco al 10% de interés anual, simple, durante 2 años ¿cuántos intereses genera? I = Co×n×i entonces 1.000×2×0,10 = 200€
Veamos la fórmula en el caso general con n años.:

A la expresión (1+ n×i) se le denomina factor de capitalización.
 Regla nemotécnica: la fórmula del carrete
Regla nemotécnica: la fórmula del carrete
Antiguamente, los pocos libros de finanzas que había, estaban en inglés y al traducirlos se mantenía la notación inglesa. Para recordar la fórmula de la capitalización simple los empleados de banca usaban un truco: si un cliente quería saber su saldo, a partir del capital inicial C, el tipo de interés r (rate) y el tiempo t (time), formaban el acrónimo CRT, de ahí surge la "fórmula del carrete".
3.2) Capitalización con interés compuesto
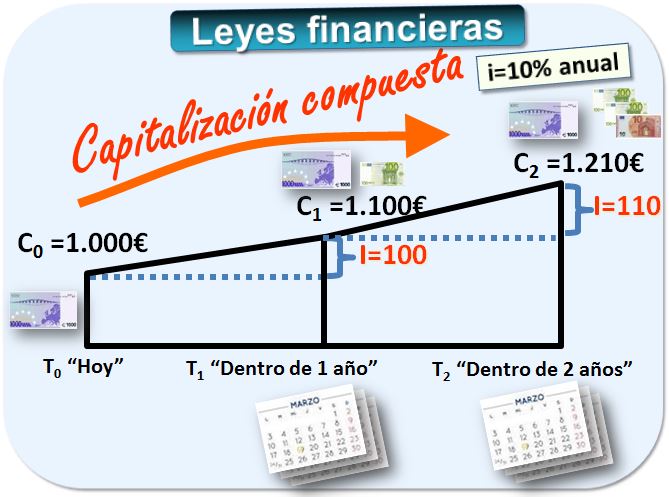
En este caso, los intereses se agregan al capital y devengan nuevos intereses. Lo vemos en el ejemplo anterior. Un plazo fijo de 1.000€ en el banco al 10% de interés anual, compuesto, durante 2 años ¿cuántos intereses genera?
Al final del año 1 ese capital se habrá convertido en 1.100€. Al final del año 2, esos 1.100€ habrán devengado 1.100 × 0,10 = 110€. Por tanto, en total hemos recibido 210€ en concepto de intereses.
3.2. a) Montante o valor final
Veamos la fórmula de la capitalización compuesta, concepto que ya utilizaban los asirios hace 4.000 años.

Hoy en día, estas fórmulas financieras se resuelven con hoja de cálculo, siendo la más utilizada la Excel de Microsoft, LibreOffice de The Document Foundation o la Hoja de Cálculo de Google. La función es VF(tasa;nper;pago;va;tipo). Aquí está la ayuda de Microsoft explicando la función: (https://support.office.microsoft.com/es-ES/article/VF...).
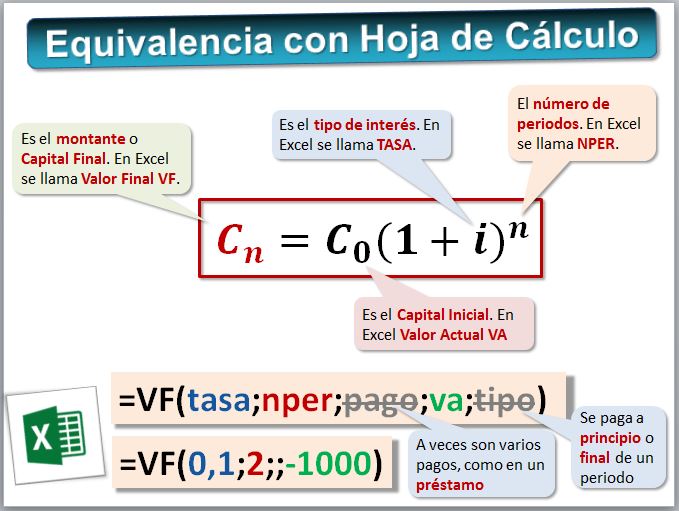
- Lo que en los libros se finanzas se llama Montante, Capital Final Cn o Valor Final, en la hoja de cálculo es VF.
- El Capital Inicial Co o Valor Actual en Excel es VA.
 Ojo, se pone en negativo, porque se considera un pago que hacemos. Es una notación de la Excel... no darle más vueltas.
Ojo, se pone en negativo, porque se considera un pago que hacemos. Es una notación de la Excel... no darle más vueltas.
- NPER es el número total de períodos de pago en una anualidad.
- El tipo de interés por periodo es TASA.
 Ojo, TASA y NPER deben ser coherentes, si son años, ambas en años y si son meses las dos en meses. En cuanto a la notación se puede poner 0,1 o 10%.
Ojo, TASA y NPER deben ser coherentes, si son años, ambas en años y si son meses las dos en meses. En cuanto a la notación se puede poner 0,1 o 10%.
- En vez de partir de un VA puede haber una serie de pagos, por ejemplo, de un préstamo que hay que devolver. Eso es una renta, lo veremos en la siguiente lección y se usa el argumento PAGO. Es decir, la misma función VF sirve para capitalizar una cuantía o para calcular el valor final de una renta.
- Esos pagos pueden ser al principio o al final del periodo, por ejemplo, se paga el primer día del mes o el último. Para esto sirve el argumento TIPO.
En nuestro ejemplo sería: calcular el Valor Final de la inversión anterior, es decir, de 1.000€ al 10% de interés compuesto, durante 2 años.
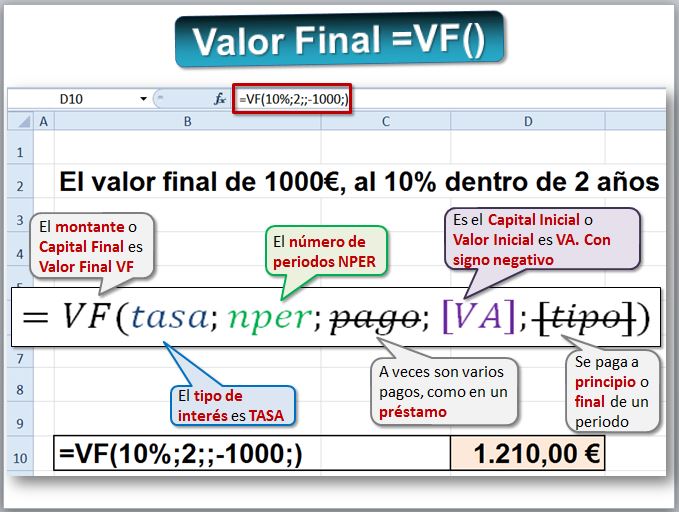
3.2. b) Tipo de interés o tasa
Muchas veces, lo que nos interesa es obtener el tipo de interés i de la operación. Por ejemplo: si me das 1.000 euros, dentro de dos años te devolveré 1.210 euros ¿cuál ha sido el tipo de interés?
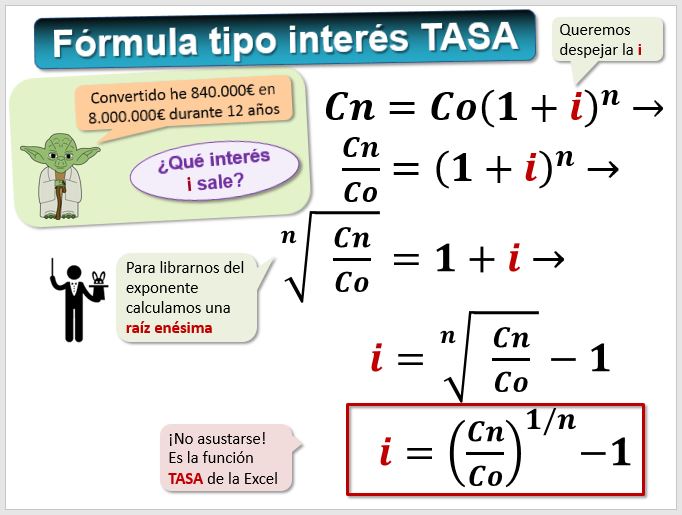
Fórmula laboriosa de calcular "a mano" pero muy sencilla de resolver con una hoja de cálculo. Además, la hoja de cálculo Excel tiene una función específica que se llama TASA, cuyos argumentos son TASA(nper;pago;va;vf;tipo;estimar) (https://support.office.com/es-ES/article/Funci%C3%B3n...). Todos los argumentos ya los hemos visto anteriormente excepto ESTIMAR, cuya utilidad real la veremos en el tema 6 sobre inversiones complejas; como la Excel calcula la tasa por un procedimiento iterativo es una especie de "pista" que podemos dar. Nuestro ejemplo sería: calcular la TASA de la inversión anterior, es decir, de 1.000€, durante 2 años sabiendo que valor final es 1.210€.
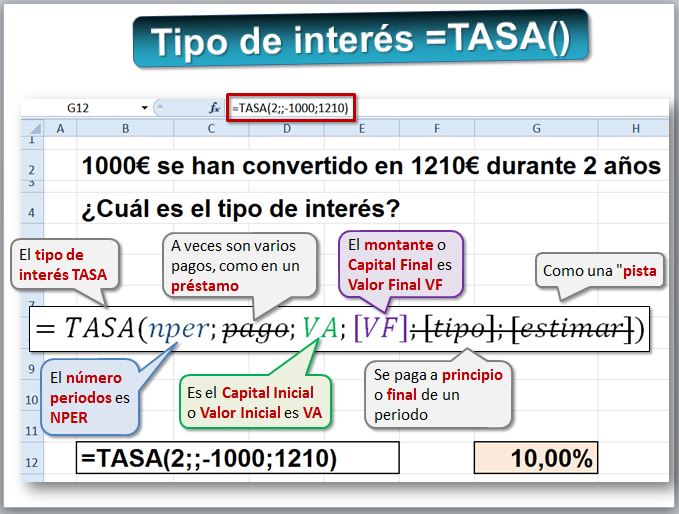
 La familia Pujol multiplicó su fortuna en 12 años, pasando de 840.000€ a 8.000.000€ ¿Cuál es el tipo de interés?
La familia Pujol multiplicó su fortuna en 12 años, pasando de 840.000€ a 8.000.000€ ¿Cuál es el tipo de interés?
Jordi Pujol  fue Presidente de la Generalidad de Cataluña entre 1980 y 2003. El 25 de julio de 2014, Jordi Pujol reconoció en un comunicado enviado a varios medios haber ocultado a la Hacienda Pública durante 34 años «un dinero ubicado en el extranjero», según sus afirmaciones procedente de su padre Florenci Pujol. En ese comunicado Pujol lamentaba no haber encontrado nunca el «momento adecuado» para la regularización de esas cantidades y pedía perdón a la opinión pública. Los fondos crecieron desde los 840.000 euros de 1980 hasta los ocho millones en 1992 según leemos en El Periódico. En el artículo pone que "la rentabilidad de estos productos era del 10% al 12%, aseguró el hijo mayor de la familia, que defendió ante la jueza que el incremento del patrimonio del clan en Andorra responde a la inversión en esos productos y a los intereses devengados". Si lo que pone en los periódicos es cierto:
fue Presidente de la Generalidad de Cataluña entre 1980 y 2003. El 25 de julio de 2014, Jordi Pujol reconoció en un comunicado enviado a varios medios haber ocultado a la Hacienda Pública durante 34 años «un dinero ubicado en el extranjero», según sus afirmaciones procedente de su padre Florenci Pujol. En ese comunicado Pujol lamentaba no haber encontrado nunca el «momento adecuado» para la regularización de esas cantidades y pedía perdón a la opinión pública. Los fondos crecieron desde los 840.000 euros de 1980 hasta los ocho millones en 1992 según leemos en El Periódico. En el artículo pone que "la rentabilidad de estos productos era del 10% al 12%, aseguró el hijo mayor de la familia, que defendió ante la jueza que el incremento del patrimonio del clan en Andorra responde a la inversión en esos productos y a los intereses devengados". Si lo que pone en los periódicos es cierto:
- ¿Son correctos los cálculos?
- ¿Es normal esa rentabilidad? Compara con una inversión similar realizada en la misma época en la bolsa de Nueva York.
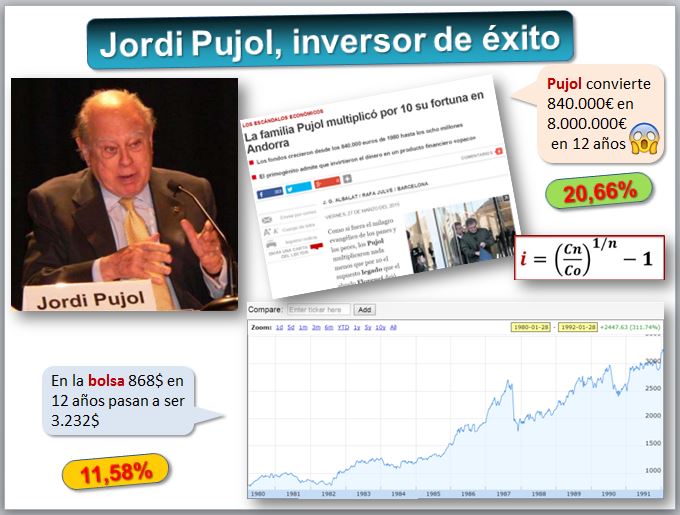
Aplicamos la fórmula i=(Cn/Co)^(1/n)-1 = (8.000.000/840.000)^(1/12)-1=20,66% muy superior al 10 o 12%.
Vamos a comparar con una inversión en bolsa, por ejemplo, en la Bolsa de Nueva York, según el índice Dow Jones. Según Macro Trends https://www.macrotrends.net/1319/dow-jones-100-year-historical-chart), el índice en 1980 cotizaba a 868$ (clic “sin inflación”) y doce años más tarde a 3.232$. En este caso i=(3.232/868)^(1/12)-1=11,58%.
3.2. c) Número de periodos
Una persona está pensando en jubilarse cuando tenga suficiente dinero ahorrado y quiere saber cuántos años le quedan. Por tanto, la incógnita es el número de periodos n y se trata nuevamente de despejarla de la ecuación. También es útil si queremos saber cuántos años nos va a costar devolver un préstamo o en cuánto tiempo amortizaremos una inversión.
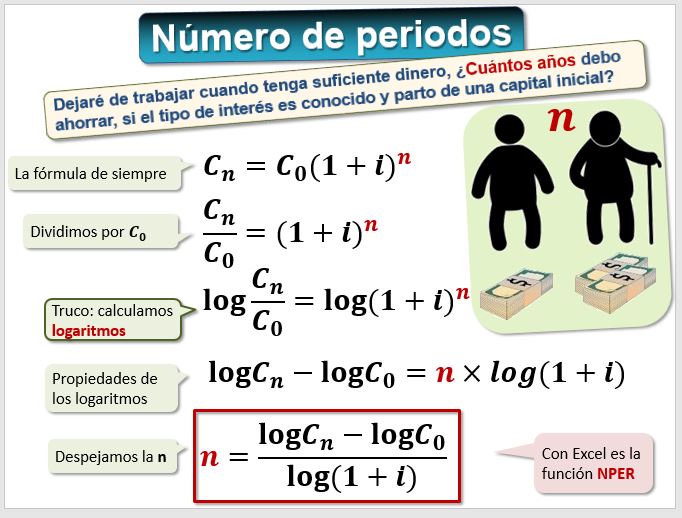
Fórmula que también es laboriosa de calcular "a mano" pero que con una hoja de cálculo es muy sencilla de calcular. En este caso la función de la hoja de cálculo Excel adecuada es NPER. En el ejemplo anterior, queremos calcular el número de periodos si el valor actual es 1.000, el final 1.210€ y el tipo es el 10% anual. La sintaxis es NPER(tasa; pago; va; vf; tipo) y la ayuda de Microsoft está en (https://support.office.com/es-ES/article/Funci%C3%B3n-NPER...).

3.2. d) Capital inicial o valor actual
Otras veces nos prometen un montante o capital final dentro de unos años y lo que queremos es saber es hoy el valor actual o capital inicial. Lo que hay que despejar es Co.
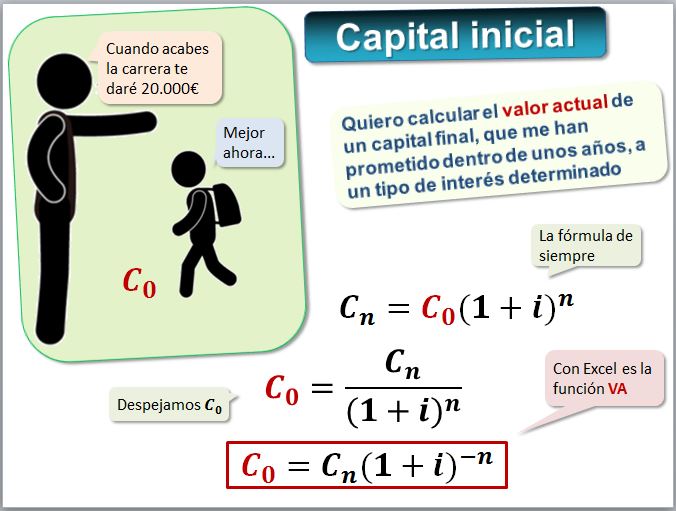
En este caso la función de la hoja de cálculo Excel adecuada es VA. En el ejemplo anterior, queremos calcular el valor actual de una inversión cuyo valor final es 1.210, el número de periodos es 2 y el tipo es el 10% anual. La sintaxis es VA(tasa;nper;pago;vf;tipo) y la ayuda de Microsoft está en (https://support.office.microsoft.com/es-ES/article/VA...).
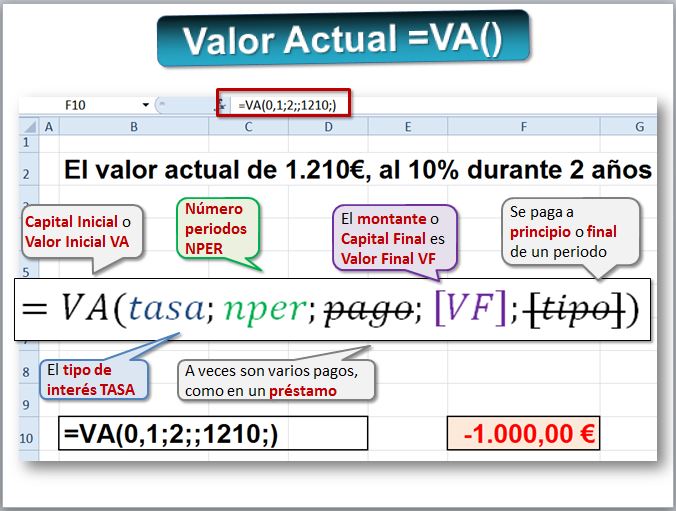
Sale con signo menos por la razón antes comentada de que la Excel considera que es un pago que hacemos. En la siguiente figura vemos las cuatro fórmulas que hemos deducido.
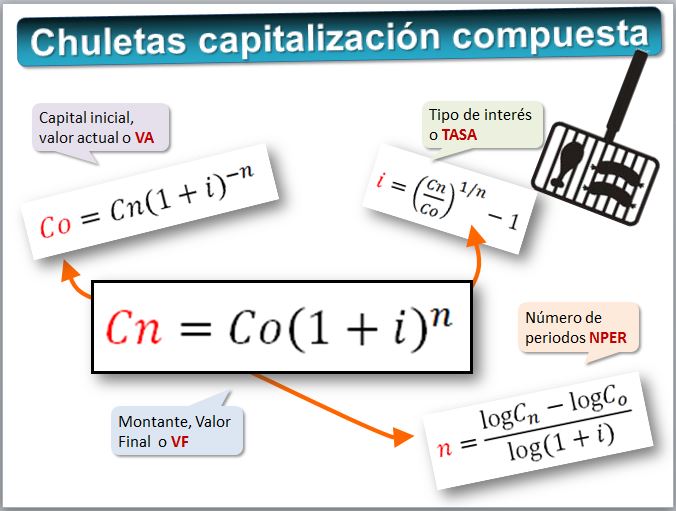
3.3) El descuento
A lo largo de la asignatura vamos a utilizar el descuento en muchas ocasiones: sirve tanto para estimar cuánto vale una patente, como para decidir si un proyecto de inversión es rentable. Otro ejemplo de descuento son los pagarés. Cualquier persona con una cuenta corriente puede ir a su banco y pedir un "talonario de pagarés". Vamos a analizar este pagaré emitido en una ocasión como medio de pago a un proveedor:
Estamos a 15 de abril y el pagaré vence dentro de seis meses, el 15 de octubre. El producto que he comprado valía 12.000€, que es el nominal (N). El proveedor va al banco con ese documento y le dan, por ejemplo, 11.500€, que es el efectivo (E). Es decir, le han descontado 500€ (D) en concepto de intereses.
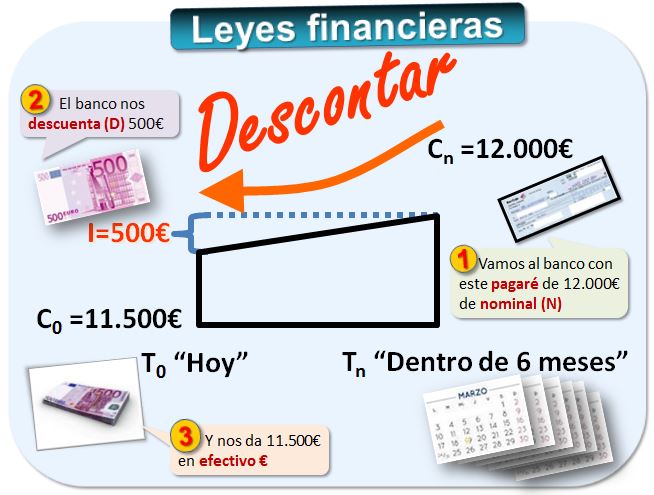
Como siempre, Cn = Co+I
En la mayoría de los libros de finanzas y en la empresa, la terminología del descuento es distinta a la de la capitalización. Suelen llamar:
- Efectivo (E) al capital inicial Co. Porque es lo que nos dan en efectivo al descontarlo.
- Nominal (N) al capital final Cn. La cantidad que figura en el pagaré.
- Y a los intereses se le llama cantidad descontada o Descuento (D).
Es decir, N = E + D
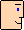 Operatoria de anticipos de facturas y descuento de pagarés
Operatoria de anticipos de facturas y descuento de pagarés
Una empresa que tiene un pagaré de un cliente puede acudir a cualquier entidad bancaria, a empresas especializadas en su descuento como Crealsa (https://www.crealsa.es/servicios/financiacion) o a plataformas electrónicas para descuento de pagarés, como Circulantis (https://circulantis.com/mercado-crowdlending) en las que cualquier particular puede adquirir uno de estos pagarés. El tipo de descuento varía en función del riesgo. Si el cliente no paga el pagaré al vencimiento, el riesgo lo asume la empresa, no la entidad financiera, excepto en el llamado descuento de pagarés sin recurso o descuento seguro. Lógicamente, el descuento es mayor.
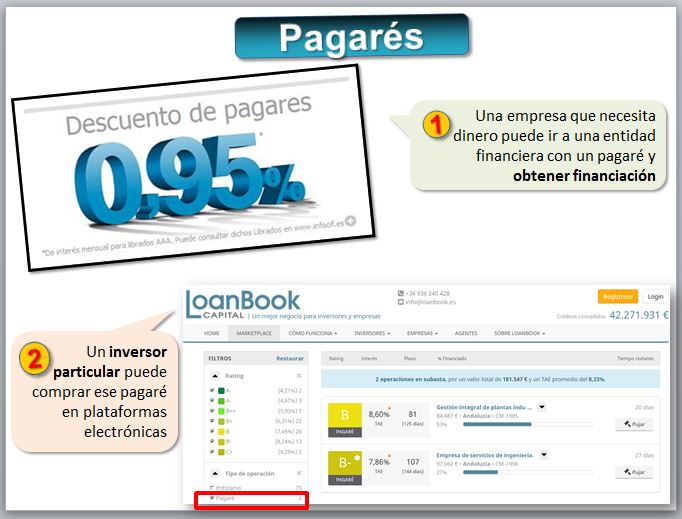
EJERCICIO: Si te ofrecen un pagaré de una empresa, ¿Qué deberías tener en cuenta? [-> concursos] Consulta en Infonif (https://infonif.economia3.com) la información que tienen de esta empresa.
En teoría, los pagarés se pueden descontar con interés simple o con interés compuesto. Y dentro del simple hay dos modalidades: descuento simple comercial y descuento simple racional. Aunque el racional es más lógico y desde el punto de vista de las matemáticas es más adecuado, en la práctica empresarial se utiliza el descuento simple comercial, que al ser el más utilizado se llama simplemente descuento comercial o descuento bancario.
3.3. a) El descuento simple racional
El descuento simple racional consiste en aplicar la ley de capitalización simple. Se aplica en las letras del tesoro y otros productos financieros que no superen el año.
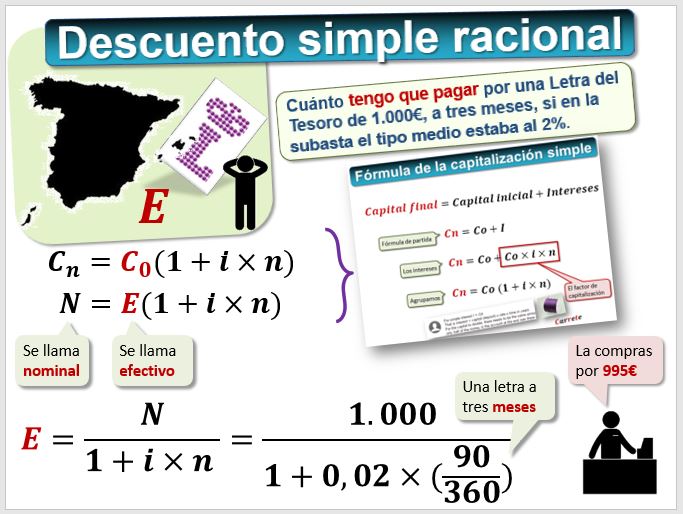
Si tenemos un pagaré cuyo nominal es 12.000€ a cobrar dentro de 1 año y la tasa de descuento que aplica la entidad es del 4,166% anual. ¿Cuánto nos darán por el pagaré hoy, es decir, cual es el efectivo, si la entidad aplica el descuento simple racional?
- N=12.000€
- n=1
- i= 4,16666%
- E=aplicando la fórmula -----> 11.520€
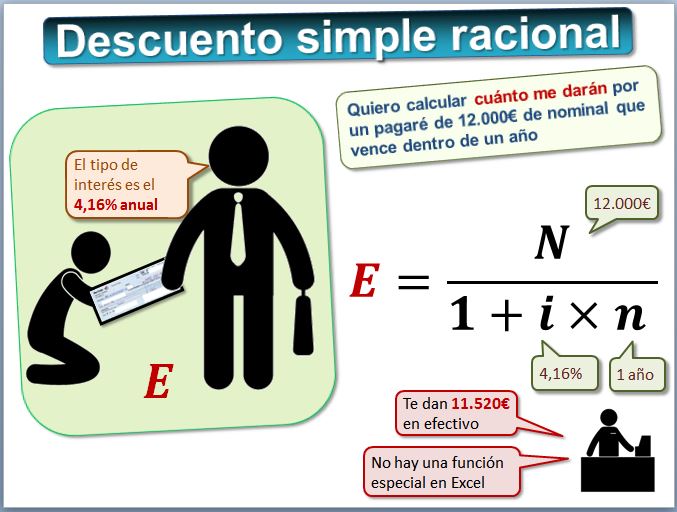
No hay una función especial de Excel que calcule el efectivo en el caso de descuento simple racional. Para calcular la tasa de descuento basta con despejar la i. Siguiendo el ejemplo anterior, tenemos un pagaré cuyo nominal es 12.000€ a cobrar dentro de 1 año. Nos han descontado 480 €, es decir el efectivo es 11.520€. ¿Cuál es la tasa de interés, si se aplica el descuento simple racional?
- N=12.000€
- n=1
- E=11.520€
- i= aplicando la fórmula -----> 4,16666%
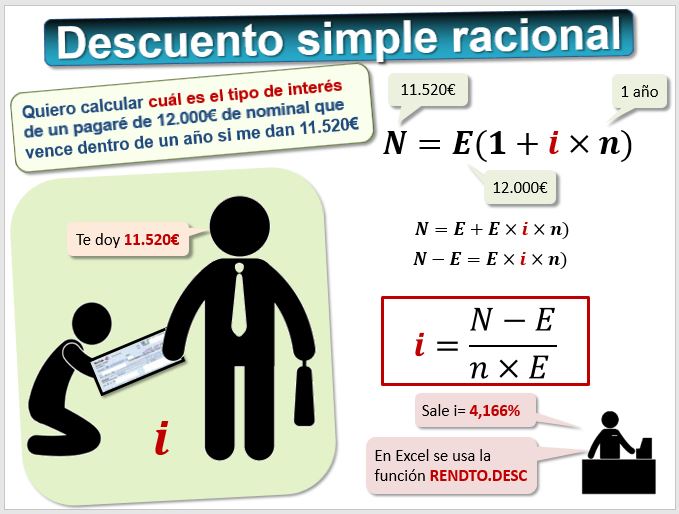
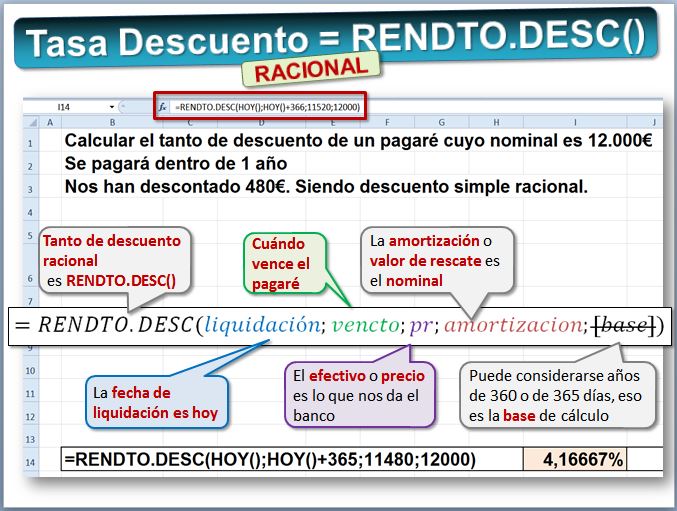
Aquí sí se puede usar la hoja de cálculo Excel, utilizando la función RENDTO.DESC. Su sintaxis es RENDTO.DESC(liquidacion;vencimiento; precio;valor_de_rescate;base). La ayuda de Excel está en (https://support.office.com/es-ES/article/Funci%C3%B3n-RENDTODESC...).
- La fecha de liquidación es aquella en la que el banco nos liquida el efecto, es decir hoy.
 se puede poner la función HOY()
se puede poner la función HOY()
- La fecha de vencimiento es cuando vence el pagaré, en este caso dentro de un año.
 se puede poner la función HOY()+ 365
se puede poner la función HOY()+ 365
- Precio o pr es el efectivo, los 11.500€ que nos da el banco.
- El valor_de_rescate es el nominal, los 12.000€.
- La base sirve para consideran si el año tiene 360 o 365 días. Se puede omitir.
Ojo, en este caso concreto si aplicamos la función TASA sale lo mismo, pero es porque se trata exactamente de un periodo de un año. Recordemos que el descuento simple racional es un caso particular de la capitalización simple, mientras que TASA aplica la ley de capitalización compuesta y como es justo un año da igual usar capitalización simple o compuesta. Pero, salvo esta excepción, no podremos usar TASA para el descuento, sino RENDTO.DESC.
3.3b) Descuento simple comercial
Sin embargo, las entidades financieras no siempre utilizan el descuento simple racional sino otra modalidad que se llama descuento simple comercial. Imagina que un cliente acude a una entidad financiera y pide un préstamo de 1.000€. El banco aplica, por ejemplo, el 10% de interés anual. Eso significa que dentro de un año tendrá que devolver 1.100€. Porque el 10% de 1.000 son 100. Sin embargo, en el descuento simple comercial las entidades financieras aplican el interés sobre los 1.100€ en vez de sobre los 1.000€. No es nada racional, porque parece lógico aplicar la tasa de interés sobre el dinero que le van a dar a uno, es decir, sobre 1.000 en vez de sobre 1.100. Pues en el descuento simple comercial las entidades hacen algo parecido y aplican una fórmula que tiene poca lógica.
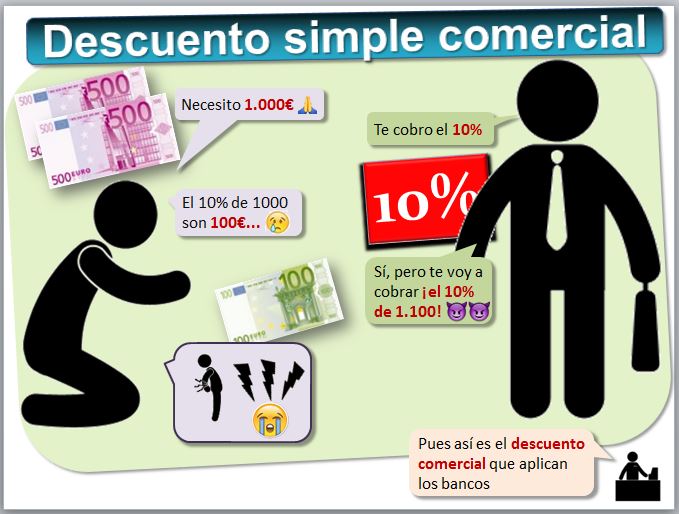
Veamos la comparación entre los dos tipos de descuentos simples: el racional y el comercial.
La ventaja del descuento comercial es su sencillez, ya que el descuento aplicado D es proporcional al nominal N. Es decir, el banco solo tiene que calcular el 10% de 10.000 y eso es inmediato. Para hacerlo bien, debería hacer una división, que sin calculadora es mucho más laborioso que una multiplicación. Otra ventaja -para el banco- es que el descuento es mayor al calcularlo de esta forma. En general, lo que nos va a interesar es conocer el tipo de interés de la operación, si son conocidos tanto el efectivo como el nominal. La fórmula que aplican los bancos para calcular el efectivo es:
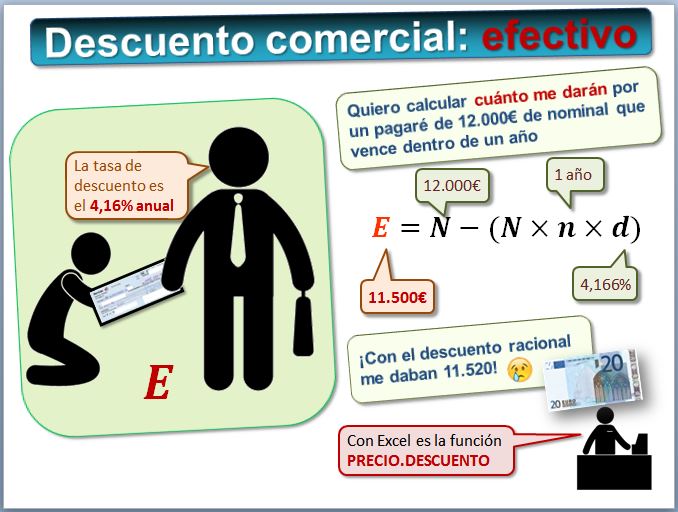
Si tenemos un pagaré cuyo nominal es 12.000€ a cobrar dentro de 1 año y la tasa de descuento que aplica la entidad es del 4,166% anual. ¿Cuánto nos darán por el pagaré hoy, es decir, cuál es el efectivo, si se aplica el descuento simple comercial?
- N=12.000€
- n=1
- d= 4,166667%
- E=aplicando la fórmula -----> 11.500€
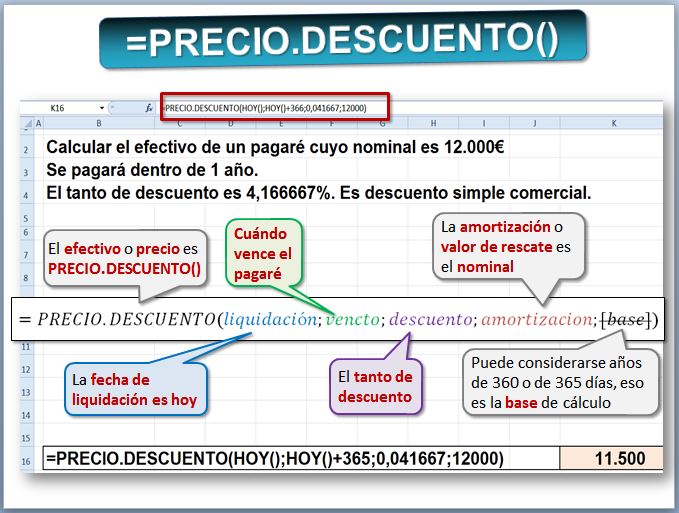
También se puede usar la hoja de cálculo Excel, utilizando la función PRECIO.DESCUENTO. Su sintaxis es PRECIO.DESCUENTO(liquidacion; vencimiento; descuento; valor_de_rescate; base). Contiene los mismos argumentos que la fórmula del, salvo descuento, que se refiere a la tasa de descuento. La ayuda de Excel está en (https://support.office.com/es-ES/article/Funci%C3%B3n-PRECIODESCUENTO...).
 "Efectivo negativo": voy a descontar un pagaré y tengo que dar dinero...
"Efectivo negativo": voy a descontar un pagaré y tengo que dar dinero...
Una paradoja que produce esta forma de interpretar las leyes financieras es que el descuento simple comercial podría dar lugar a obtener un efectivo negativo, si el periodo de tiempo es grande. Por ejemplo, si tenemos un pagaré cuyo nominal es 12.000€ que vence dentro de 11 años y nos lo descuentan al 10% anual, el efectivo es -1.200€. Es decir, que tendríamos que entregarle al banco el pagaré y en vez de darnos dinero le tendríamos que pagar 1.200€, lo cual es absurdo.

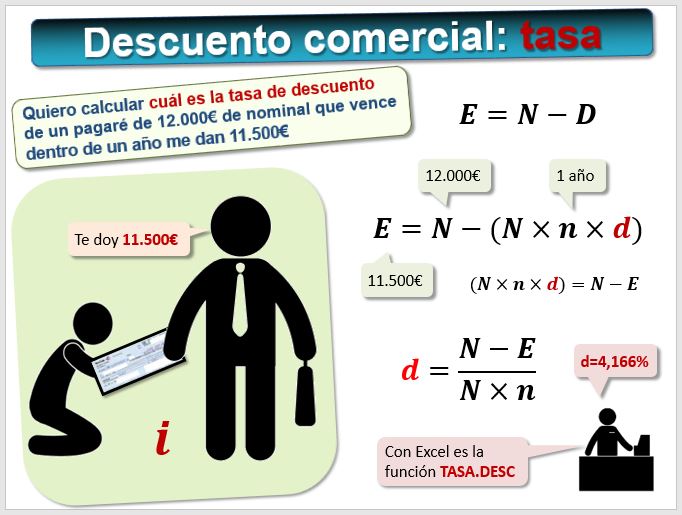
En otras ocasiones la incógnita es el tanto de descuento. En el ejemplo anterior tenemos un pagaré cuyo nominal es 12.000€ a cobrar dentro de 1 año. Nos han descontado 500€. ¿Cuál es el tanto de descuento, si se aplica el descuento simple comercial?
- N=12.000€
- n=1
- D=500€
- d= aplicando la fórmula -----> 4,16666%
Nótese que, como es interés simple, es proporcional. Es decir, si por el pagaré de 12.000€ nos descuentan 250€ en medio año, el tanto de descuento sigue siendo del 4,16666%.
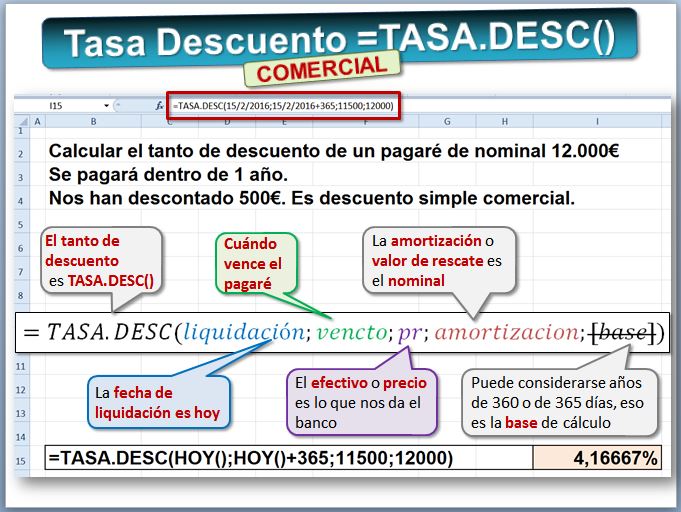
También se puede usar la hoja de cálculo Excel, utilizando la función TASA.DESC. Su sintaxis es TASA.DESC(liquidación; vencimiento; precio; valor_de_rescate; base). La ayuda de Excel está en (https://support.office.com/es-ES/article/Funci%C3%B3n-TASADESC...).
- La fecha de liquidación es aquella en la que el banco nos liquida el efecto, es decir hoy.
 se puede poner la función HOY()
se puede poner la función HOY()
- La fecha de vencimiento es cuando vence el pagaré, en este caso dentro de un año.
 se puede poner la función HOY()+ 365
se puede poner la función HOY()+ 365
- Precio o pr es el efectivo, los 11.500€ que nos da el banco.
- El valor_de_rescate es el nominal, los 12.000€.
- El argumento base se utiliza porque los bancos pueden realizar sus cálculos considerando que el año tiene 360 o 365 días. Se puede omitir. Vemos un ejemplo a continuación.
 Año civil y comercial
Año civil y comercial
El año civil tiene 365 días. El llamado año comercial es de 360 días. Las entidades financieras con frecuencia realizan sus cálculos considerando que el año tiene 360 días. Su justificación es que es más sencillo realizar los cálculos considerando que el año tiene 12 meses iguales, de 30 días cada uno. Ello es más ventajoso para el banco, como podemos comprobar fácilmente al sustituir el plazo n por días/365 o por días/360. Por ejemplo, si tenemos un pagaré cuyo nominal es 12.000€ a cobrar dentro de 90 días, siendo la tasa de descuento que aplica la entidad del 10% anual. ¿Cuánto nos darán por el pagaré hoy?, es decir, ¿cuál es el efectivo, aplicando descuento simple comercial?
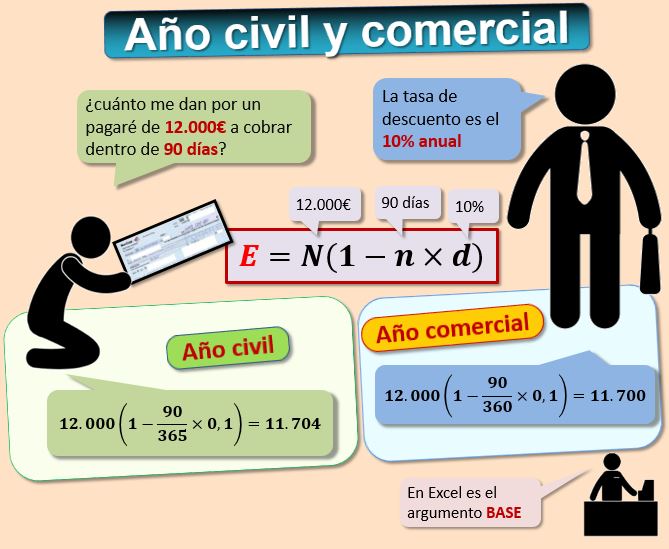
Comparemos el año comercial de 360 días con el año civil de 365 días. La fórmula:
- Con año comercial E=N(1-n*d) = 12.000(1-90/360*0,1) = 11.700€
- Con año civil E=N(1-n*d) = 12.000(1-0,1*90/365*0,1) = 11.704,11€
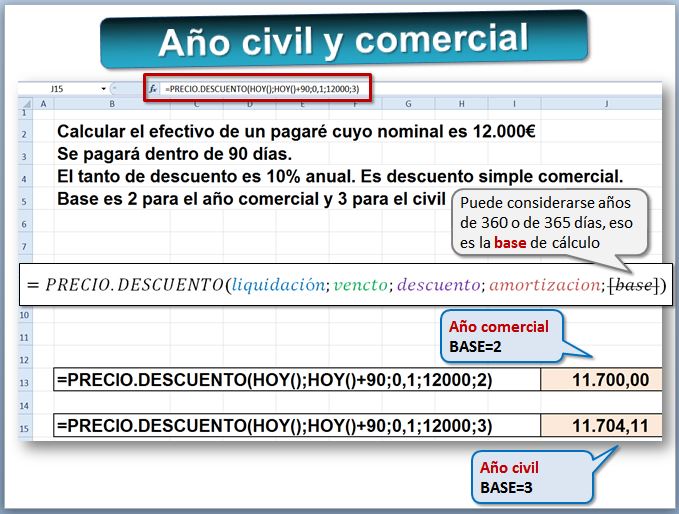
Este es el significado del argumento base en la hoja de cálculo.
- Si en base ponemos el número 2, la función lo calcula como año comercial.
- Si base es 3 entonces se entiende que queremos el cálculo considerando el año civil.
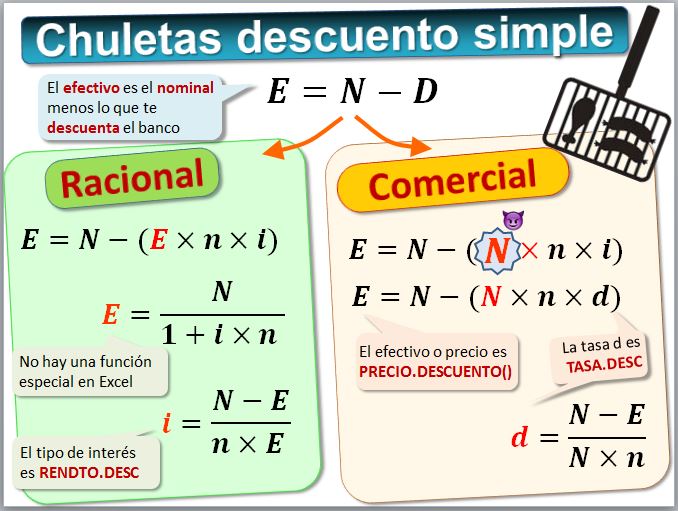
Veamos, a modo de resumen, la chuleta del descuento simple, racional y comercial, junto las funciones de Excel.
 El papel pelota
El papel pelota
El papel pelota es una forma delictiva de conseguir liquidez, que consiste en descontar un pagaré en el banco sin que haya detrás una transacción comercial, con el único fin de conseguir fondos. "Le damos un pagaré a un proveedor y éste nos da otro pagaré por el mismo importe; ambos vamos a descontarlos al banco y así tenemos efectivo los dos"... lo malo si te pillan [caso Pescanova 150 empresas, 25 países, 4 años, agujero de 2.400 millones €] [noticias estafa pagarés].
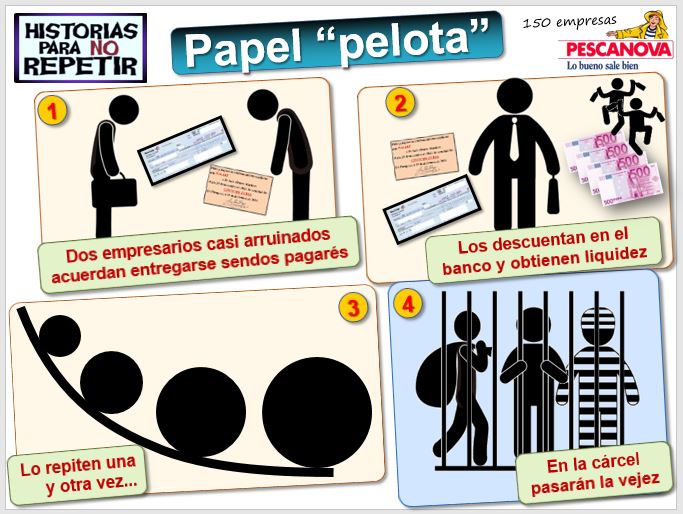
Aunque hemos puesto como ejemplos de descuento el pagaré o las letras del Tesoro, en la lección 6 veremos cómo los proyectos de inversión, en los que tras una inversión inicial obtenemos unos flujos de dinero, proporcionan un buen ejemplo de uso del descuento, ya que dichos flujos de caja se descuentan para obtener su Valor Actual.
3.4) Descuento hiperbólico
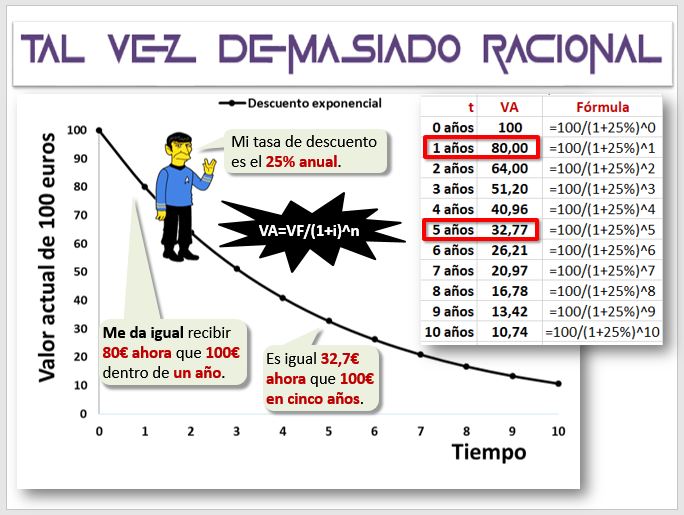
Hemos visto el descuento racional, que se deriva de las fórmulas financieras basadas en la función exponencial Co=Cn/(1+i)n. Hemos visto como los bancos aplican unas fórmulas distintas. Pero ¿las personas realmente descontamos así? La siguiente figura muestra el comportamiento de alguien muy racional, el vulcaniano Mr Spock. Mr Spock tiene una tasa de descuento del 25% y se comporta siguiendo las fórmulas vistas en clase, es decir, el llamado "descuento exponencial". A Mr Spock le da igual recibir 80€ ahora que 100€ dentro de un año, lo que coincide con lo predicho por la fórmula. Si le ofrecemos 60€ ahora dirá que no le interesa, que prefiere esperar. Y si le ofrecemos 90€ ahora dirá que sí. Si tiene que esperar 5 años, prefiere exactamente 32,77€, tal y como predice la fórmula del descuento.
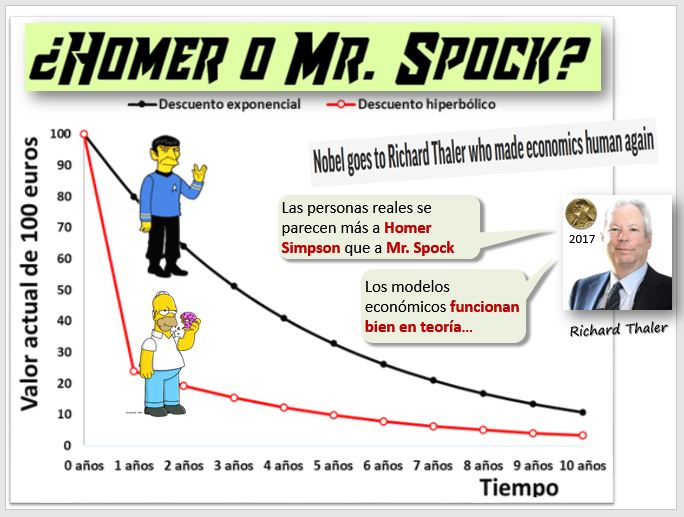
Pero la mayoría de la gente real no es así. Las personas prefieren disponer del dinero más en el presente de lo que corresponde según la formula. Los estudios empíricos han demostrado que se comportan más como el Homer Simpson de la figura. El impaciente y gastador Homer se conforma con 24€ ahora, no quiere esperar a tener los 100€ un año, dinero que dedicará a comprar rosquillas. Y realmente a Homer le da casi igual esperar 8 años que 10, lo ve muy lejano. Homer opera según el llamado "descuento hiperbólico ", fórmula que incluye un parámetro nuevo, β, que se refiere al sesgo por el presente.

Numerosos autores han estudiado cómo realmente toman las decisiones financieras las personas, echando mano de la Psicología. Dos de los más notables recibieron sendos Premios Nobel de Economía, y hablan de la "ceguera inducida por la teoría", es decir, alguien (el también Premio Nobel, Paul Samuelson  en su artículo publicado en 1937) pensó que el descuento exponencial era una solución muy elegante y nadie posteriormente se lo cuestionó, dándolo por bueno. Nos referimos al psicólogo Daniel Kahneman
en su artículo publicado en 1937) pensó que el descuento exponencial era una solución muy elegante y nadie posteriormente se lo cuestionó, dándolo por bueno. Nos referimos al psicólogo Daniel Kahneman  (Premio Nobel en 2002) y al economista Richard Thaler
(Premio Nobel en 2002) y al economista Richard Thaler  (Premio Nobel en 2017). La comparación de Homer vs Mr Spock es de este último autor.
(Premio Nobel en 2017). La comparación de Homer vs Mr Spock es de este último autor.
Esto no significa que las fórmulas matemáticas que hemos estudiado estén mal, ya que son las que usan las entidades financieras para calcular los intereses que recibirás por un depósito o las cuotas de una hipoteca. Pero conocer cómo funciona realmente el cerebro humano, no tan racional sino padeciendo sesgos o anomalías, como el bautizado como "sesgo hiperbólico" o "sesgo del presente" proporciona oportunidades para las entidades financieras, que lo utilizan para ofrecer productos financieros más atractivos para sus clientes. Por ejemplo, bancos que ofrecen un elevado interés... pero solo el primer año (los Homer se fijan sobre todo en eso). A Homer le encanta que le regalen algo ya, por ejemplo, un juego de sartenes al abrir una cuenta en el banco o 300€. Al "comprar hoy y pagar mañana" parece que no estamos haciendo gasto y aumentamos las compras, muchas de ellas innecesarias. Si la TAE es 0, ¿de qué viven estas empresas financieras BNPL (Buy Now Pay Later)? Como último ejemplo vemos cómo una empresa logra vender mucho más cara proporcionalmente una suscripción trimestral que anual, con lo que obtiene más beneficio de las personas hiperbólicas.

En el experimento de la golosina  se dio a varios niños la oportunidad de obtener una golosina ya o dos golosinas si esperaban 15 minutos. Años más tarde se observó que los niños pacientes alcanzaban mejores calificaciones en la escuela, conseguían mejores trabajos y llevaban una vida mejor. En el siguiente vídeo puedes ver su funcionamiento. Es un ejemplo de aplicación del descuento hiperbólico, que también se ha testado con animales.
se dio a varios niños la oportunidad de obtener una golosina ya o dos golosinas si esperaban 15 minutos. Años más tarde se observó que los niños pacientes alcanzaban mejores calificaciones en la escuela, conseguían mejores trabajos y llevaban una vida mejor. En el siguiente vídeo puedes ver su funcionamiento. Es un ejemplo de aplicación del descuento hiperbólico, que también se ha testado con animales.
 Para seguir aprendiendo
Para seguir aprendiendo
En realidad, no existe el Premio Nobel de Economía, sino el Premio del Banco de Suecia en Ciencias Económicas en memoria de Alfred Nobel  . Recomendamos la lectura de dos libros de autores premiados. Todo lo que he aprendido con la Psicología Económica, de Richard Thaler y Pensar rápido, pensar despacio, de su mentor Daniel Kahneman. Ambos libros ofrecen un punto de vista complementario al que ofrecen los libros clásicos de Economía.
. Recomendamos la lectura de dos libros de autores premiados. Todo lo que he aprendido con la Psicología Económica, de Richard Thaler y Pensar rápido, pensar despacio, de su mentor Daniel Kahneman. Ambos libros ofrecen un punto de vista complementario al que ofrecen los libros clásicos de Economía.

, ex-presidente de La Generalidad de Cataluña creció desde los 840.000 euros en 1980 hasta los ocho millones en 1992. Como economistas podemos preguntarnos si esa rentabilidad es normal o es poco creíble. La Cuenta Nómina de Bankinter ofrece unos atractivos intereses ¿qué opinión te merece? Plataformas electrónicas como Circulantis.com ofrecen a inversores particulares la posibilidad de adquirir pagarés de empresas ¿Es una buena opción?
. Por ese motivo, en la figura hemos añadido a Homer Simpson y Mr Spock, de los que hablaremos al finalizar la lección.
Puedes descargar una hoja de cálculo con los ejemplos que veremos en teoría -> [01-Teoria.xls].